11 changed files with 524 additions and 22 deletions
Unified View
Diff Options
-
BINWork 1/report/Work1_report.pdf
-
+103 -12Work 1/report/Work1_report.tex
-
BINWork 1/scripts/Prob1_responce_20s.png
-
BINWork 1/scripts/Prob1_responce_90s.png
-
BINWork 1/scripts/Prob2_20s_Ts0.1.png
-
BINWork 1/scripts/Prob2b_20s_Ts0.1.png
-
+13 -10Work 1/scripts/Problem1.m
-
+79 -0Work 1/scripts/Problem2a.m
-
+88 -0Work 1/scripts/Problem2b.m
-
+202 -0Work 1/scripts/problem1_data.csv
-
+39 -0Work 1/scripts/sample_data.m
BIN
Work 1/report/Work1_report.pdf
View File
+ 103
- 12
Work 1/report/Work1_report.tex
View File
| @@ -96,41 +96,44 @@ | |||||
| Το σύστημα που μελετάται περιγράφεται από τη γραμμικοποιημένη διαφορική εξίσωση: | Το σύστημα που μελετάται περιγράφεται από τη γραμμικοποιημένη διαφορική εξίσωση: | ||||
| \[ | \[ | ||||
| mL^2 \ddot{q}(t) + c \dot{q}(t) + mgL q(t) = u(t) | |||||
| mL^2 \ddot{q}(t) + c \dot{q}(t) + mgL q(t) = u(t) | |||||
| \] | \] | ||||
| όπου $q(t)$ είναι η γωνία του εκκρεμούς, $u(t)$ η ροπή εισόδου, και $m$, $L$, $c$, $g$ φυσικές σταθερές του συστήματος. | όπου $q(t)$ είναι η γωνία του εκκρεμούς, $u(t)$ η ροπή εισόδου, και $m$, $L$, $c$, $g$ φυσικές σταθερές του συστήματος. | ||||
| Ορίζοντας ως διάνυσμα κατάστασης: | Ορίζοντας ως διάνυσμα κατάστασης: | ||||
| \[ | \[ | ||||
| x(t) = \begin{bmatrix} q(t) \\ \dot{q}(t) \end{bmatrix} | |||||
| x(t) = \begin{bmatrix} q(t) \\ \dot{q}(t) \end{bmatrix} | |||||
| \] | \] | ||||
| οι εξισώσεις κατάστασης γράφονται ως: | οι εξισώσεις κατάστασης γράφονται ως: | ||||
| \[ | \[ | ||||
| \dot{x}(t) = A x(t) + B u(t) | |||||
| \dot{x}(t) = A x(t) + B u(t) | |||||
| \] | \] | ||||
| όπου: | όπου: | ||||
| \[ | \[ | ||||
| A = | |||||
| \begin{bmatrix} | |||||
| 0 & 1 \\ | |||||
| -\frac{g}{L} & -\frac{c}{mL^2} | |||||
| \end{bmatrix}, | |||||
| \quad | |||||
| B = \begin{bmatrix} 0 \\ \frac{1}{mL^2} \end{bmatrix} | |||||
| A = | |||||
| \begin{bmatrix} | |||||
| 0 & 1 \\ | |||||
| -\frac{g}{L} & -\frac{c}{mL^2} | |||||
| \end{bmatrix}, | |||||
| \quad | |||||
| B = \begin{bmatrix} 0 \\ \frac{1}{mL^2} \end{bmatrix} | |||||
| \] | \] | ||||
| Η συνάρτηση μεταφοράς του συστήματος προκύπτει από την αρχική εξίσωση ως: | Η συνάρτηση μεταφοράς του συστήματος προκύπτει από την αρχική εξίσωση ως: | ||||
| \[ | \[ | ||||
| G(s) = \frac{Q(s)}{U(s)} = \frac{1}{mL^2 s^2 + c s + mgL}. | |||||
| G(s) = \frac{Q(s)}{U(s)} = \frac{1}{mL^2 s^2 + c s + mgL} | |||||
| \] | \] | ||||
| Για την προσομοίωση χρησιμοποιήθηκε ημιτονική είσοδος $u(t) = A_0 \sin(\omega t)$, με $A_0 = 4$ και $\omega = 2$. | Για την προσομοίωση χρησιμοποιήθηκε ημιτονική είσοδος $u(t) = A_0 \sin(\omega t)$, με $A_0 = 4$ και $\omega = 2$. | ||||
| Οι υπόλοιπες παράμετροι ήταν $m = 0.75$, $L = 1.25$, $c = 0.15$, $g = 9.81$. | Οι υπόλοιπες παράμετροι ήταν $m = 0.75$, $L = 1.25$, $c = 0.15$, $g = 9.81$. | ||||
| Ο αρχικός χρόνος προσομοίωσης ορίστηκε σε $20$ δευτερόλεπτα, όπως ζητείται στην εκφώνηση. | Ο αρχικός χρόνος προσομοίωσης ορίστηκε σε $20$ δευτερόλεπτα, όπως ζητείται στην εκφώνηση. | ||||
| \paragraph*{Σημείωση:} | |||||
| Η προσομοίωση του Θέματος 1 χρησίμευσε όχι μόνο για την παρατήρηση της δυναμικής του συστήματος, αλλά και για την παραγωγή των δεδομένων που χρησιμοποιήθηκαν στο Θέμα 2 για την εκτίμηση των παραμέτρων. Η ακρίβεια των αποτελεσμάτων του Θέματος 2 επιβεβαιώνει τη σωστή ρύθμιση και υλοποίηση της προσομοίωσης. | |||||
| \subsection*{Παρατήρηση Συμπεριφοράς Συστήματος} | \subsection*{Παρατήρηση Συμπεριφοράς Συστήματος} | ||||
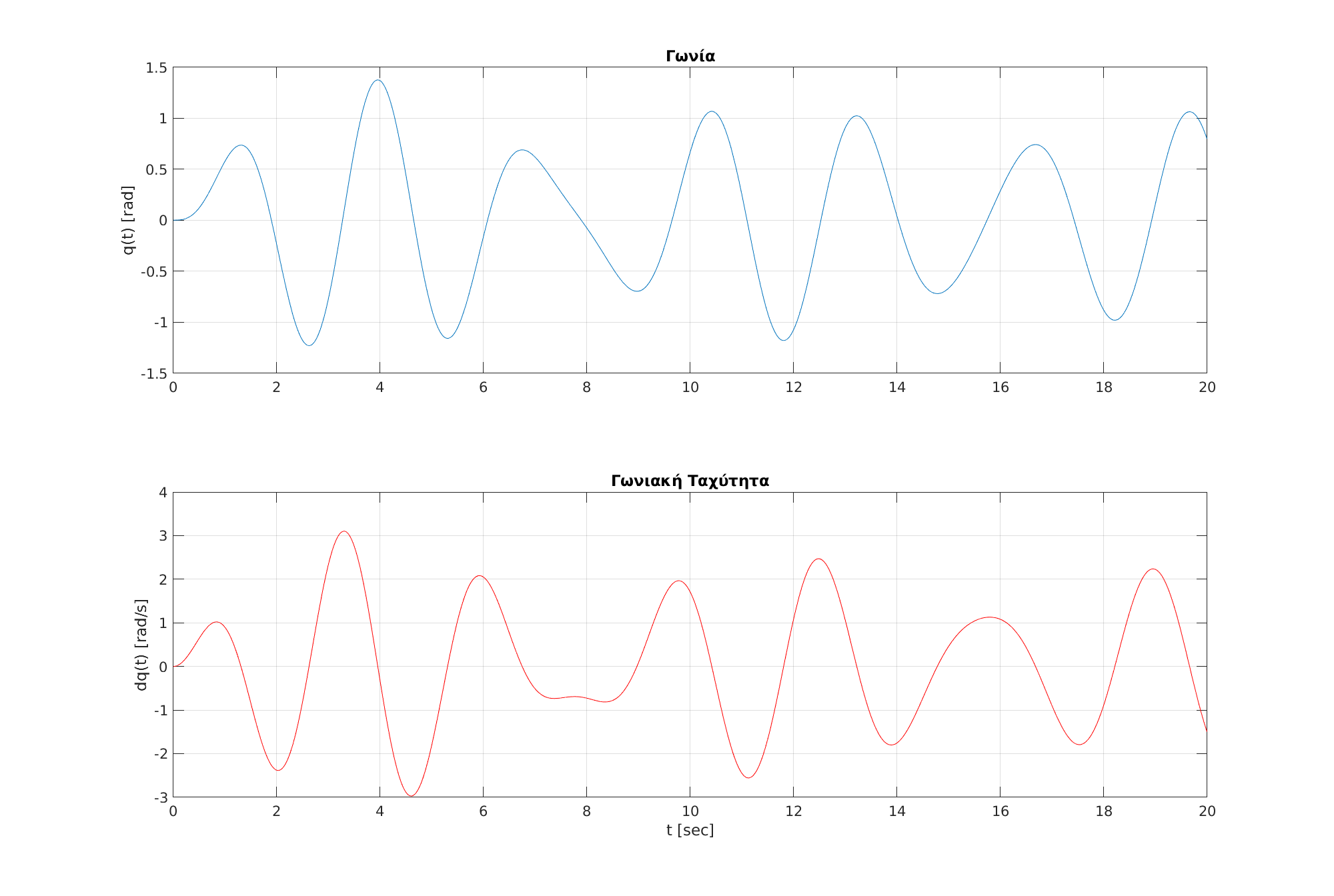
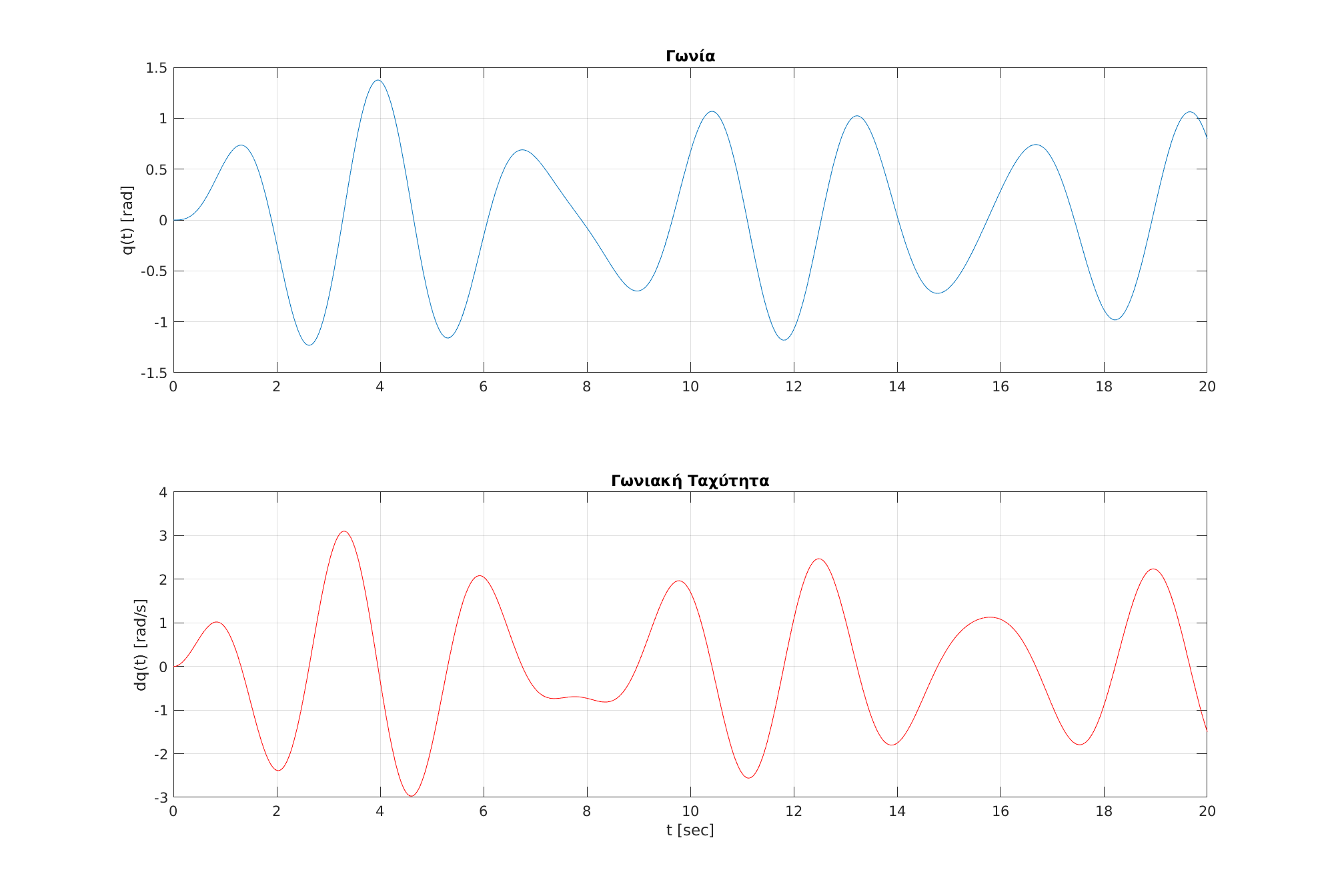
| Το σύστημα παρουσίασε περιοδική απόκριση, η οποία όμως δεν σταθεροποιήθηκε γρήγορα. | |||||
| Βλέπουμε ότι το σύστημα παρουσιάζει περιοδική απόκριση, η οποία όμως δεν σταθεροποιείται γρήγορα. | |||||
| Όπως φαίνεται στο Σχήμα~\ref{fig:20s}, το πλάτος των ταλαντώσεων συνεχίζει να μεταβάλλεται ακόμη και μετά από 20 δευτερόλεπτα, γεγονός που δείχνει ότι το σύστημα βρίσκεται ακόμη σε μεταβατική κατάσταση. | Όπως φαίνεται στο Σχήμα~\ref{fig:20s}, το πλάτος των ταλαντώσεων συνεχίζει να μεταβάλλεται ακόμη και μετά από 20 δευτερόλεπτα, γεγονός που δείχνει ότι το σύστημα βρίσκεται ακόμη σε μεταβατική κατάσταση. | ||||
| Η καθυστερημένη σύγκλιση οφείλεται κυρίως: | Η καθυστερημένη σύγκλιση οφείλεται κυρίως: | ||||
| @@ -149,5 +152,93 @@ G(s) = \frac{Q(s)}{U(s)} = \frac{1}{mL^2 s^2 + c s + mgL}. | |||||
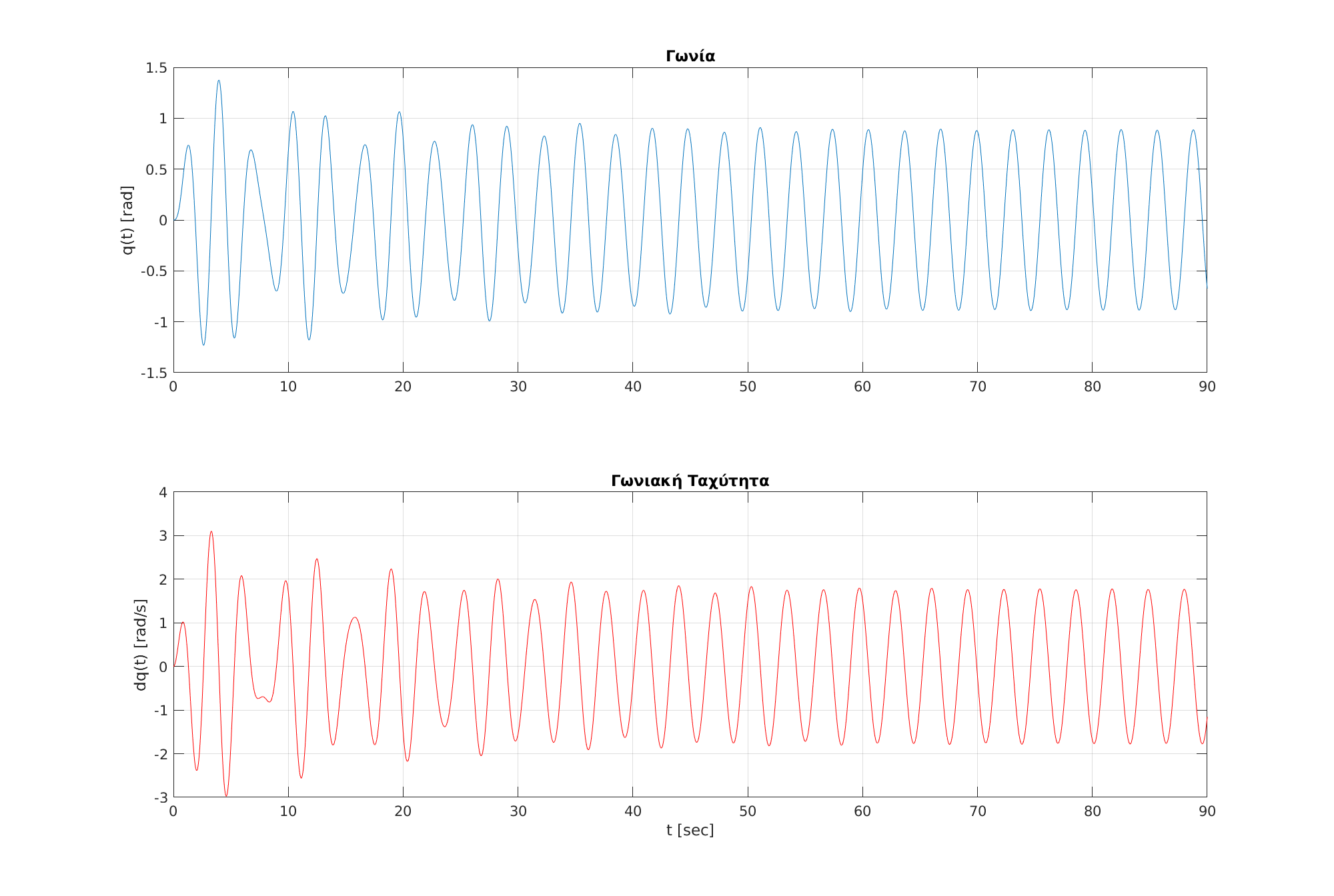
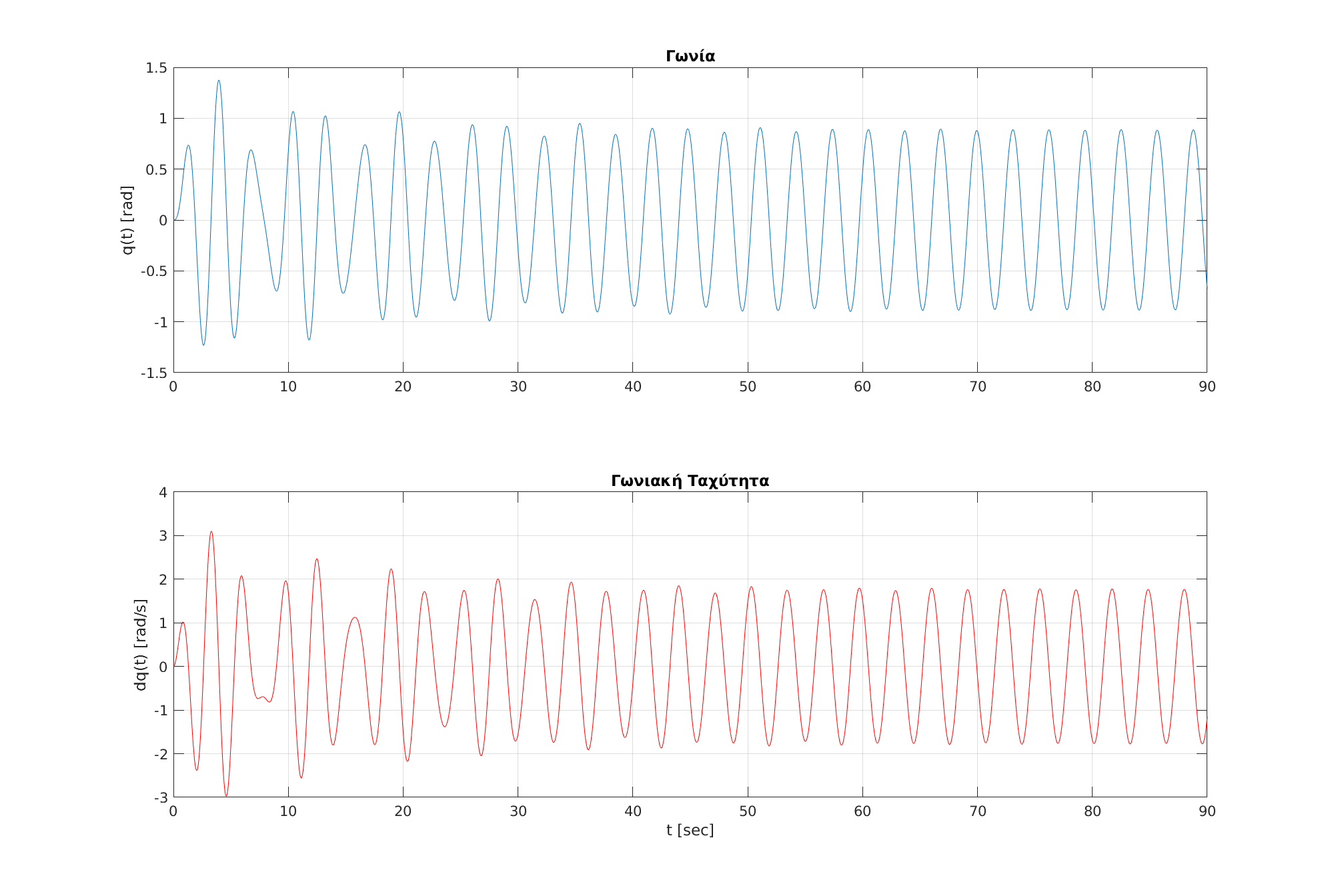
| Απόκριση του συστήματος για $t \in [0, 90]$ sec. Το σύστημα σταθεροποιείται σε περιοδική συμπεριφορά μετά τα $50$ sec. | Απόκριση του συστήματος για $t \in [0, 90]$ sec. Το σύστημα σταθεροποιείται σε περιοδική συμπεριφορά μετά τα $50$ sec. | ||||
| } | } | ||||
| \section{Θέμα 2 – Εκτίμηση Παραμέτρων με τη Μέθοδο Ελαχίστων Τετραγώνων} | |||||
| Η εξίσωση που περιγράφει τη δυναμική του εκκρεμούς είναι της μορφής: | |||||
| \[ | |||||
| mL^2 \ddot{q}(t) + c \dot{q}(t) + mgL q(t) = u(t) | |||||
| \] | |||||
| Η παραπάνω εξίσωση είναι γραμμική ως προς τις παραμέτρους, επομένως μπορεί να αναδιατυπωθεί ως: | |||||
| \[ | |||||
| u(t) = \theta_1 \ddot{q}(t) + \theta_2 \dot{q}(t) + \theta_3 q(t) | |||||
| \quad \text{με} \quad | |||||
| \theta = \begin{bmatrix} mL^2 \\ c \\ mgL \end{bmatrix} | |||||
| \] | |||||
| Στόχος του παρόντος ερωτήματος είναι η εκτίμηση του διανύσματος $\theta$ με χρήση μετρήσεων από την έξοδο του συστήματος και της εισόδου $u(t)$, εφαρμόζοντας τη μέθοδο των ελαχίστων τετραγώνων. | |||||
| \subsection{Υποερώτημα (α)} | |||||
| Στο πρώτο υποερώτημα θεωρείται ότι είναι διαθέσιμες μετρήσεις όλων των μεταβλητών κατάστασης, δηλαδή $q(t)$, $\dot{q}(t)$ και $\ddot{q}(t)$, καθώς και της εισόδου $u(t)$. | |||||
| Δημιουργείται λοιπόν το πρόβλημα παλινδρόμησης: | |||||
| \[ | |||||
| u = X \theta | |||||
| \quad \text{όπου} \quad | |||||
| X = \begin{bmatrix} \ddot{q}_1 & \dot{q}_1 & q_1 \\ \ddot{q}_2 & \dot{q}_2 & q_2 \\ \vdots & \vdots & \vdots \end{bmatrix} | |||||
| \] | |||||
| Η λύση του προκύπτει με τον γνωστό τύπο: | |||||
| \[ | |||||
| \hat{\theta} = (X^T X)^{-1} X^T u | |||||
| \] | |||||
| Αφού εκτιμηθούν οι παράμετροι, χρησιμοποιούνται για να υπολογιστεί η επιτάχυνση $\ddot{q}_{\text{est}}(t)$ και στη συνέχεια η ανακατασκευή της απόκρισης $q_{\text{est}}(t)$ με αριθμητική ολοκλήρωση. | |||||
| Η διαδικασία υλοποιείται με ένα απλό βρόχο επανάληψης (for loop), όπου για κάθε χρονικό βήμα $k$ υπολογίζονται διαδοχικά: | |||||
| \[ | |||||
| \dot{q}_{\text{est}}(k) = \dot{q}_{\text{est}}(k-1) + T_s \cdot \ddot{q}_{\text{est}}(k-1) | |||||
| \] | |||||
| \[ | |||||
| q_{\text{est}}(k) = q_{\text{est}}(k-1) + T_s \cdot \dot{q}_{\text{est}}(k-1) | |||||
| \] | |||||
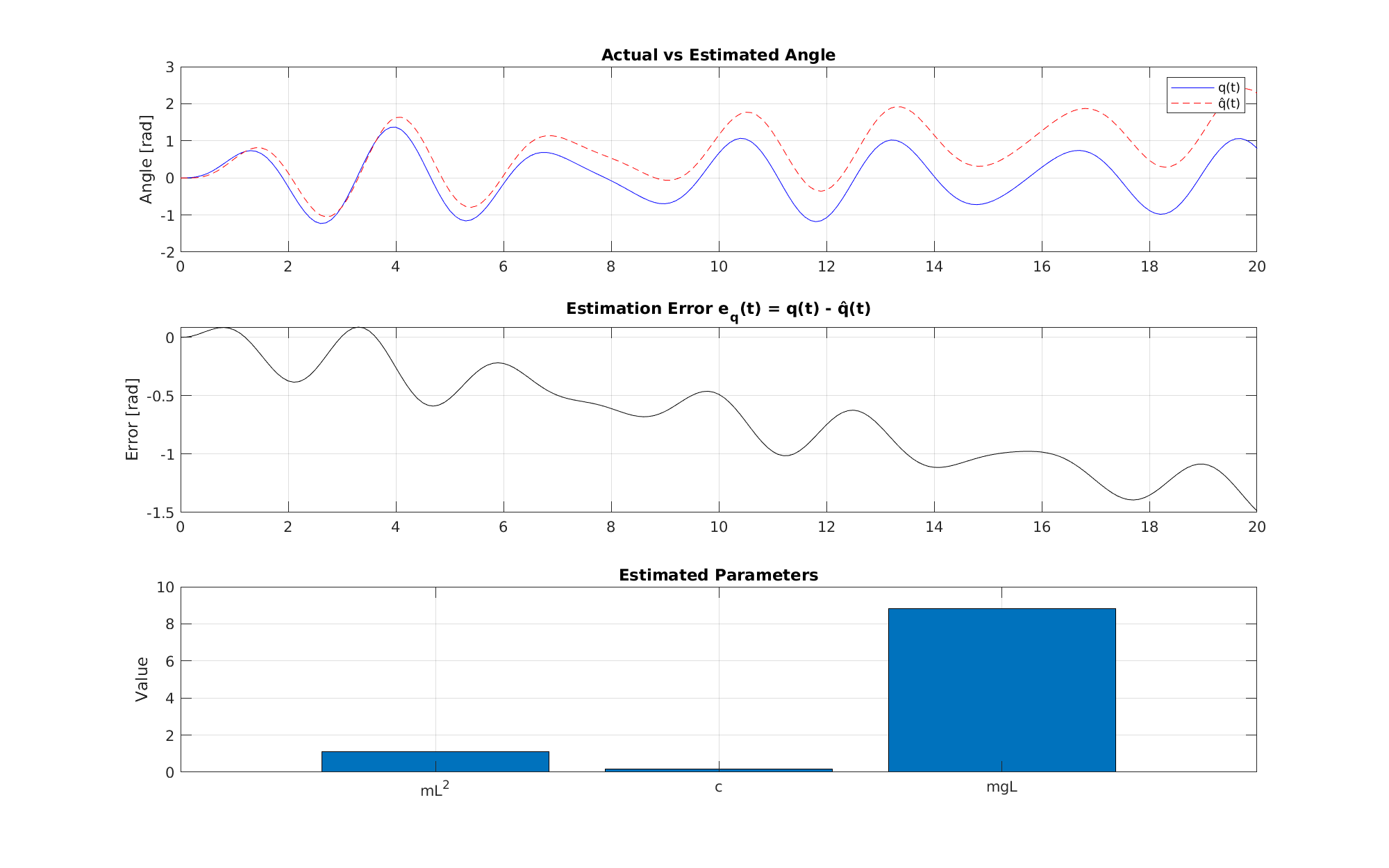
| Στο Σχήμα~\ref{fig:prob2a} παρουσιάζονται η πραγματική και η εκτιμώμενη γωνία, καθώς και το σφάλμα $e_q(t)$ μεταξύ τους. | |||||
| \InsertFigure{!ht}{1}{fig:prob2a}{../scripts/Prob2_20s_Ts0.1.png}{ | |||||
| Αποτελέσματα εκτίμησης παραμέτρων με χρήση όλων των μεταβλητών κατάστασης. | |||||
| } | |||||
| \paragraph*{Συμπεράσματα:} | |||||
| Η εκτίμηση παρουσιάζει υψηλή ακρίβεια, με σχετικό σφάλμα μικρότερο του 6\% για όλες τις παραμέτρους. | |||||
| Ο αλγόριθμος κατάφερε να ανακατασκευάσει την απόκριση με μικρό σφάλμα, επιβεβαιώνοντας τη θεωρητική εγκυρότητα της μεθόδου. | |||||
| \vspace{1em} | |||||
| \subsection{Υποερώτημα (β)} | |||||
| Στη δεύτερη περίπτωση θεωρούμε ότι διαθέσιμες είναι μόνο οι μετρήσεις της γωνίας $q(t)$ και της εισόδου $u(t)$. | |||||
| Οι παράγωγοι $\dot{q}(t)$ και $\ddot{q}(t)$ υπολογίζονται αριθμητικά από το σήμα $q(t)$ με χρήση διαφορικών τελεστών 2ης τάξης ακρίβειας (κεντρικών διαφορών): | |||||
| \[ | |||||
| \dot{q}(t_k) \approx \frac{q_{k+1} - q_{k-1}}{2T_s}, | |||||
| \quad | |||||
| \ddot{q}(t_k) \approx \frac{q_{k+1} - 2q_k + q_{k-1}}{T_s^2} | |||||
| \] | |||||
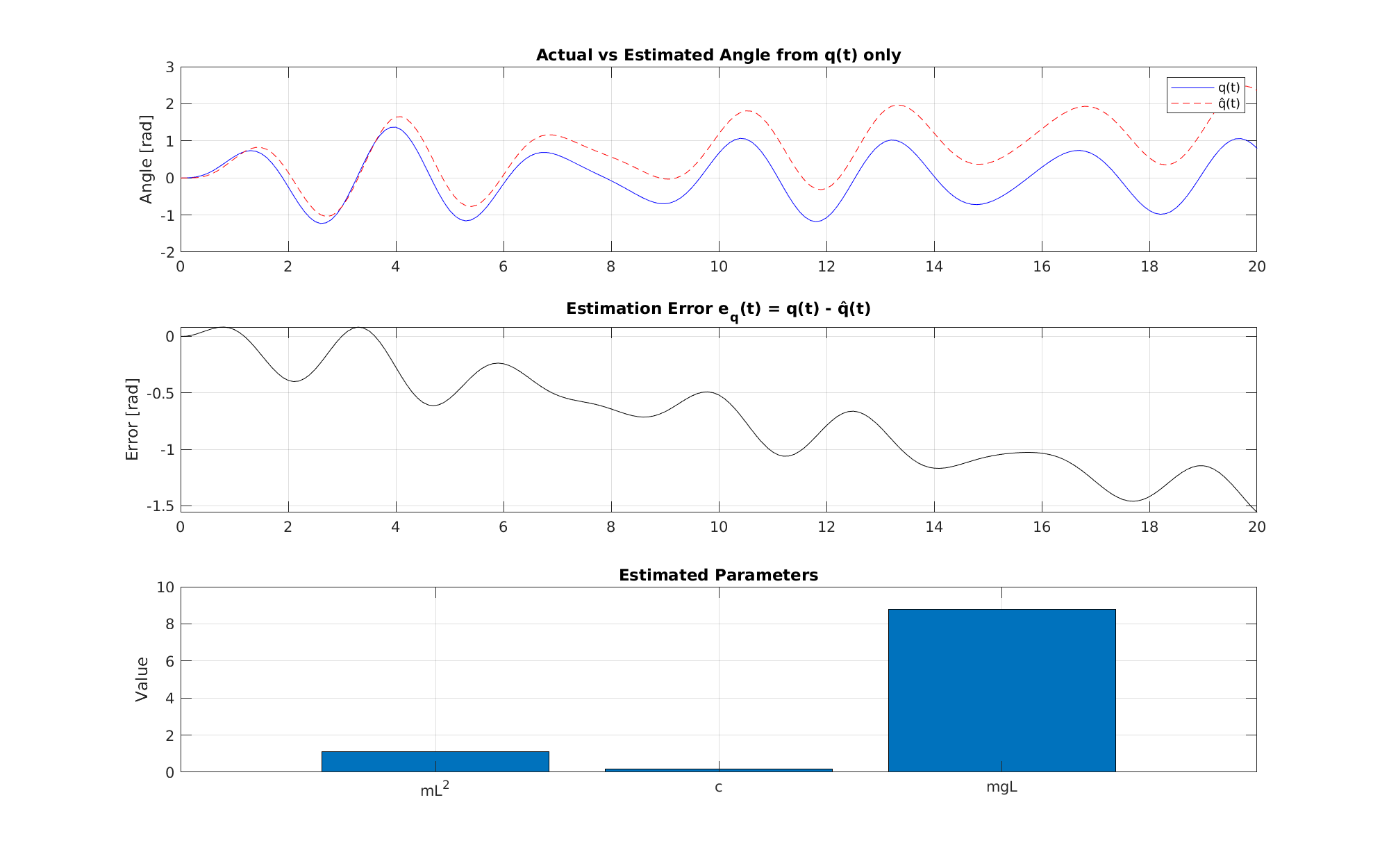
| Ακολουθείται η ίδια διαδικασία παλινδρόμησης με την περίπτωση (α), όπως και η ανακατασκευή της απόκρισης. Το Σχήμα~\ref{fig:prob2b} δείχνει τα αντίστοιχα αποτελέσματα. | |||||
| \InsertFigure{!ht}{1}{fig:prob2b}{../scripts/Prob2b_20s_Ts0.1.png}{ | |||||
| Αποτελέσματα εκτίμησης παραμέτρων με χρήση μόνο του $q(t)$ και του $u(t)$. | |||||
| } | |||||
| \paragraph*{Συμπεράσματα:} | |||||
| Παρά τον περιορισμό στη διαθέσιμη πληροφορία, η εκτίμηση παρέμεινε εξαιρετικά ακριβής, με μικρές αποκλίσεις από την πραγματική τιμή. Το γεγονός αυτό δείχνει την ισχυρή ταυτοποιησιμότητα του συστήματος και τη δυνατότητα εφαρμογής της μεθόδου ακόμη και με ελλιπή δεδομένα. | |||||
| \vspace{1em} | |||||
| \subsection{Σύγκριση των δύο περιπτώσεων} | |||||
| Ο παρακάτω πίνακας συγκρίνει τις πραγματικές και εκτιμώμενες τιμές για τα δύο υποερωτήματα: | |||||
| \begin{center} | |||||
| \begin{tabular}{c|c|c|c|c|c} | |||||
| Παράμετρος & Πραγματική Τιμή & Εκτίμηση 2α & Σφάλμα 2α (\%) & Εκτίμηση 2β & Σφάλμα 2β (\%) \\ | |||||
| \hline | |||||
| $mL^2$ & 1.1719 & 1.1007 & $-6.07\%$ & 1.0977 & $-6.33\%$ \\ | |||||
| $c$ & 0.1500 & 0.1690 & $+12.7\%$ & 0.1569 & $+4.6\%$ \\ | |||||
| $mgL$ & 9.1969 & 8.8157 & $-4.15\%$ & 8.8002 & $-4.31\%$ \\ | |||||
| \end{tabular} | |||||
| \end{center} | |||||
| Παρατηρούμε ότι και στις δύο περιπτώσεις οι εκτιμήσεις είναι ακριβείς και σταθερές, με τις αποκλίσεις να κυμαίνονται σε χαμηλά επίπεδα. Μάλιστα, το γεγονός ότι τα σφάλματα είναι αντίστοιχα ακόμα και όταν χρησιμοποιείται λιγότερη πληροφορία (περίπτωση 2β), αποτελεί ένδειξη για τη σταθερότητα και αξιοπιστία της μεθόδου. Ταυτόχρονα, αναδεικνύει την ιδιαίτερη σημασία της επιλογής σήματος διέγερσης και της ποιότητας των δεδομένων. | |||||
| \end{document} | \end{document} | ||||
BIN
Work 1/scripts/Prob1_responce_20s.png
View File
BIN
Work 1/scripts/Prob1_responce_90s.png
View File
BIN
Work 1/scripts/Prob2_20s_Ts0.1.png
View File
BIN
Work 1/scripts/Prob2b_20s_Ts0.1.png
View File
+ 13
- 10
Work 1/scripts/Problem1.m
View File
| @@ -1,3 +1,5 @@ | |||||
| % === Problem 1: Simulation of the responce === | |||||
| % Parameters | % Parameters | ||||
| m = 0.75; | m = 0.75; | ||||
| L = 1.25; | L = 1.25; | ||||
| @@ -6,9 +8,9 @@ g = 9.81; | |||||
| A0 = 4; | A0 = 4; | ||||
| omega = 2; | omega = 2; | ||||
| % Time span | |||||
| % Time span for 20s simulation | |||||
| tspan = [0 20]; | tspan = [0 20]; | ||||
| dt = 1e-3; | |||||
| dt = 1e-4; | |||||
| t_eval = 0:dt:20; | t_eval = 0:dt:20; | ||||
| % ODE Function | % ODE Function | ||||
| @@ -20,28 +22,29 @@ odefun = @(t, x) [ | |||||
| x0 = [0; 0]; % Initial conditions | x0 = [0; 0]; % Initial conditions | ||||
| [t, x] = ode45(odefun, t_eval, x0); % Solve | [t, x] = ode45(odefun, t_eval, x0); % Solve | ||||
| % Plots | |||||
| % Plots for 20 sec | |||||
| figure('Name', 'System responce', 'Position', [100, 100, 1280, 860]); | figure('Name', 'System responce', 'Position', [100, 100, 1280, 860]); | ||||
| subplot(2,1,1); | subplot(2,1,1); | ||||
| plot(t, x(:,1)); ylabel('q(t) [rad]'); grid on; title('Γωνία'); | plot(t, x(:,1)); ylabel('q(t) [rad]'); grid on; title('Γωνία'); | ||||
| subplot(2,1,2); | subplot(2,1,2); | ||||
| plot(t, x(:,2), 'r'); ylabel('dq(t) [rad/s]'); xlabel('t [sec]'); grid on; title('Γωνιακή Ταχύτητα'); | plot(t, x(:,2), 'r'); ylabel('dq(t) [rad/s]'); xlabel('t [sec]'); grid on; title('Γωνιακή Ταχύτητα'); | ||||
| saveas(gcf, 'Prob1_responce_20s.png'); | saveas(gcf, 'Prob1_responce_20s.png'); | ||||
| % === Sampling for Problem 2 === | |||||
| Ts = 0.1; % Sampling period | |||||
| sample_data(t, x, Ts, A0, omega, 'problem1_data.csv'); | |||||
| % Time span | |||||
| % --- Extended simulation to 90 sec --- | |||||
| tspan = [0 90]; | tspan = [0 90]; | ||||
| t_eval = 0:dt:90; | t_eval = 0:dt:90; | ||||
| x0 = [0; 0]; % Initial conditions | |||||
| [t, x] = ode45(odefun, t_eval, x0); % Solve | |||||
| x0 = [0; 0]; | |||||
| [t, x] = ode45(odefun, t_eval, x0); | |||||
| % Plots | |||||
| % Plots for 90 sec | |||||
| figure('Name', 'System responce', 'Position', [100, 100, 1280, 860]); | figure('Name', 'System responce', 'Position', [100, 100, 1280, 860]); | ||||
| subplot(2,1,1); | subplot(2,1,1); | ||||
| plot(t, x(:,1)); ylabel('q(t) [rad]'); grid on; title('Γωνία'); | plot(t, x(:,1)); ylabel('q(t) [rad]'); grid on; title('Γωνία'); | ||||
| subplot(2,1,2); | subplot(2,1,2); | ||||
| plot(t, x(:,2), 'r'); ylabel('dq(t) [rad/s]'); xlabel('t [sec]'); grid on; title('Γωνιακή Ταχύτητα'); | plot(t, x(:,2), 'r'); ylabel('dq(t) [rad/s]'); xlabel('t [sec]'); grid on; title('Γωνιακή Ταχύτητα'); | ||||
| saveas(gcf, 'Prob1_responce_90s.png'); | |||||
| saveas(gcf, 'Prob1_responce_90s.png'); | |||||
+ 79
- 0
Work 1/scripts/Problem2a.m
View File
| @@ -0,0 +1,79 @@ | |||||
| % === Problem 2: Parameter Estimation using Least Squares === | |||||
| % True data for comparison | |||||
| m = 0.75; | |||||
| L = 1.25; | |||||
| c_true = 0.15; | |||||
| g = 9.81; | |||||
| mL2_true = m * L^2; | |||||
| mgL_true = m * g * L; | |||||
| theta_true = [mL2_true; c_true; mgL_true]; | |||||
| % Load sampled data from Problem 1 | |||||
| data = readtable('problem1_data.csv'); | |||||
| t = data.t; | |||||
| q = data.q; | |||||
| dq = data.dq; | |||||
| ddq = data.ddq; | |||||
| u = data.u; | |||||
| % Build regression matrix X and target vector y = u | |||||
| X = [ddq, dq, q]; % columns correspond to coefficients of [mL^2, c, mgL] | |||||
| y = u; | |||||
| % Least Squares estimation: theta_hat = [mL^2; c; mgL] | |||||
| theta_hat = (X' * X) \ (X' * y); | |||||
| % Extract individual parameters (optional interpretation) | |||||
| mL2_est = theta_hat(1); | |||||
| c_est = theta_hat(2); | |||||
| mgL_est = theta_hat(3); | |||||
| % Reconstruct ddq_hat using the estimated parameters | |||||
| ddq_hat = (1 / mL2_est) * (u - c_est * dq - mgL_est * q); | |||||
| % Numerical integration to recover dq̂(t) and q̂(t) | |||||
| Ts = t(2) - t(1); | |||||
| N = length(t); | |||||
| dq_hat = zeros(N,1); | |||||
| q_hat = zeros(N,1); | |||||
| % Initial conditions | |||||
| dq_hat(1) = dq(1); | |||||
| q_hat(1) = q(1); | |||||
| for k = 2:N | |||||
| dq_hat(k) = dq_hat(k-1) + Ts * ddq_hat(k-1); | |||||
| q_hat(k) = q_hat(k-1) + Ts * dq_hat(k-1); | |||||
| end | |||||
| % Estimation error | |||||
| e_q = q - q_hat; | |||||
| % === Plots === | |||||
| figure('Name', 'Problem 2 - LS Estimation', 'Position', [100, 100, 1280, 800]); | |||||
| subplot(3,1,1); | |||||
| plot(t, q, 'b', t, q_hat, 'r--'); | |||||
| legend('q(t)', 'q̂(t)'); | |||||
| title('Actual vs Estimated Angle'); | |||||
| ylabel('Angle [rad]'); | |||||
| grid on; | |||||
| subplot(3,1,2); | |||||
| plot(t, e_q, 'k'); | |||||
| title('Estimation Error e_q(t) = q(t) - q̂(t)'); | |||||
| ylabel('Error [rad]'); | |||||
| grid on; | |||||
| subplot(3,1,3); | |||||
| bar(["mL^2", "c", "mgL"], theta_hat); | |||||
| title('Estimated Parameters'); | |||||
| ylabel('Value'); | |||||
| grid on; | |||||
| saveas(gcf, 'Prob2_20s_Ts0.1.png'); | |||||
| fprintf(' Actual Parameters: mL^2=%f, c=%f, mgL=%f\n', theta_true(1), theta_true(2), theta_true(3)); | |||||
| fprintf('Estimated Parameters: mL^2=%f, c=%f, mgL=%f\n', theta_hat(1), theta_hat(2), theta_hat(3)); | |||||
+ 88
- 0
Work 1/scripts/Problem2b.m
View File
| @@ -0,0 +1,88 @@ | |||||
| % === Problem 2b: Estimation using only q(t) and u(t) === | |||||
| % True parameter values | |||||
| m = 0.75; | |||||
| L = 1.25; | |||||
| c_true = 0.15; | |||||
| g = 9.81; | |||||
| mL2_true = m * L^2; | |||||
| mgL_true = m * g * L; | |||||
| theta_true = [mL2_true; c_true; mgL_true]; | |||||
| % Load sampled data | |||||
| data = readtable('problem1_data.csv'); | |||||
| t = data.t; | |||||
| q = data.q; | |||||
| u = data.u; | |||||
| Ts = t(2) - t(1); | |||||
| N = length(t); | |||||
| % Compute dq and ddq using central differences | |||||
| dq = zeros(N, 1); | |||||
| ddq = zeros(N, 1); | |||||
| for k = 2:N-1 | |||||
| dq(k) = (q(k+1) - q(k-1)) / (2 * Ts); | |||||
| ddq(k) = (q(k+1) - 2*q(k) + q(k-1)) / Ts^2; | |||||
| end | |||||
| % Build regression matrix and output vector | |||||
| X = [ddq, dq, q]; | |||||
| y = u; | |||||
| % Least Squares estimation | |||||
| theta_hat = (X' * X) \ (X' * y); | |||||
| % Parameter extraction | |||||
| mL2_est = theta_hat(1); | |||||
| c_est = theta_hat(2); | |||||
| mgL_est = theta_hat(3); | |||||
| % Reconstruct ddq_hat from estimated parameters | |||||
| ddq_hat = (1 / mL2_est) * (u - c_est * dq - mgL_est * q); | |||||
| % Integrate to get dq_hat and q_hat | |||||
| dq_hat = zeros(N,1); | |||||
| q_hat = zeros(N,1); | |||||
| dq_hat(1) = dq(1); | |||||
| q_hat(1) = q(1); | |||||
| for k = 2:N | |||||
| dq_hat(k) = dq_hat(k-1) + Ts * ddq_hat(k-1); | |||||
| q_hat(k) = q_hat(k-1) + Ts * dq_hat(k-1); | |||||
| end | |||||
| % Estimation error | |||||
| e_q = q - q_hat; | |||||
| % === Plots === | |||||
| figure('Name', 'Problem 2b - LS Estimation from q only', 'Position', [100, 100, 1280, 800]); | |||||
| subplot(3,1,1); | |||||
| plot(t, q, 'b', t, q_hat, 'r--'); | |||||
| legend('q(t)', 'q̂(t)'); | |||||
| title('Actual vs Estimated Angle from q(t) only'); | |||||
| ylabel('Angle [rad]'); | |||||
| grid on; | |||||
| subplot(3,1,2); | |||||
| plot(t, e_q, 'k'); | |||||
| title('Estimation Error e_q(t) = q(t) - q̂(t)'); | |||||
| ylabel('Error [rad]'); | |||||
| grid on; | |||||
| subplot(3,1,3); | |||||
| bar(["mL^2", "c", "mgL"], theta_hat); | |||||
| title('Estimated Parameters'); | |||||
| ylabel('Value'); | |||||
| grid on; | |||||
| % Save figure | |||||
| saveas(gcf, 'Prob2b_20s_Ts0.1.png'); | |||||
| % Print results | |||||
| fprintf(' Actual Parameters: mL^2=%f, c=%f, mgL=%f\n', theta_true(1), theta_true(2), theta_true(3)); | |||||
| fprintf('Estimated Parameters: mL^2=%f, c=%f, mgL=%f\n', theta_hat(1), theta_hat(2), theta_hat(3)); | |||||
+ 202
- 0
Work 1/scripts/problem1_data.csv
View File
| @@ -0,0 +1,202 @@ | |||||
| t,q,dq,ddq,u | |||||
| 0,0,0,0,0 | |||||
| 0.1,0.00112730370377742,0.0336536743050961,0.657669343872878,0.794677323180245 | |||||
| 0.2,0.00883130084628362,0.130095105060834,1.23031152735571,1.5576733692346 | |||||
| 0.3,0.0288384132623469,0.277086967848714,1.6472957578342,2.25856989358014 | |||||
| 0.4,0.0653184832567522,0.456177260208145,1.85826392239339,2.86942436359809 | |||||
| 0.5,0.120381192475091,0.64441963262565,1.82183441394098,3.36588393923159 | |||||
| 0.6,0.19366224583284,0.816729955124557,1.5387129073771,3.72815634386891 | |||||
| 0.7,0.28233042826436,0.947731422726794,1.01198704123085,3.94179891995384 | |||||
| 0.8,0.381118481108189,1.01514724688817,0.281130829714293,3.99829441216602 | |||||
| 0.9,0.48271784224916,1.00127150126433,-0.606890939324855,3.89539052351278 | |||||
| 1,0.578248293996883,0.894322024572221,-1.54403616041735,3.63718970730273 | |||||
| 1.1,0.658338384140432,0.691502504394097,-2.46777849195839,3.23398561527836 | |||||
| 1.2,0.713750689364397,0.398398200996943,-3.35626893527373,2.7018527222046 | |||||
| 1.3,0.735600305235625,0.0284599263544737,-4.00825914367234,2.06200548728586 | |||||
| 1.4,0.71736732967013,-0.396782279453475,-4.38489881755735,1.33995260062362 | |||||
| 1.5,0.655285365929061,-0.849118356836855,-4.531083639236,0.564480032239469 | |||||
| 1.6,0.547892565795632,-1.29622623806606,-4.3244857319699,-0.23349657371032 | |||||
| 1.7,0.397254908342504,-1.70407791327366,-3.73168898607231,-1.02216440810733 | |||||
| 1.8,0.209300361028653,-2.04006080855522,-2.86613213766537,-1.77008177317941 | |||||
| 1.9,-0.00731550766185135,-2.27387198043844,-1.72922293231809,-2.44743156377088 | |||||
| 2,-0.241223605675537,-2.38106324008954,-0.381252753564326,-3.02720998123171 | |||||
| 2.1,-0.478944231224866,-2.34680237646659,1.08356113140267,-3.48630308965435 | |||||
| 2.2,-0.705829245460168,-2.16426570569947,2.58237734005865,-3.80640829555806 | |||||
| 2.3,-0.906890486294884,-1.83629821096442,3.93455844050654,-3.97476401453386 | |||||
| 2.4,-1.06860614272453,-1.37787653165824,5.11374520668299,-3.98465843534336 | |||||
| 2.5,-1.17918434708735,-0.81284329382283,6.09389607575295,-3.83569709865255 | |||||
| 2.6,-1.22882359069265,-0.17295878351365,6.62469772469187,-3.53381862288061 | |||||
| 2.7,-1.21221585705102,0.503754630673891,6.74037610639779,-3.09105795022395 | |||||
| 2.8,-1.12820436234541,1.17582411838087,6.533191358181,-2.52506655148928 | |||||
| 2.9,-0.978860954057995,1.79981035847128,5.85182622072886,-1.85840871765503 | |||||
| 3,-0.770999283563291,2.33562906493079,4.75245091059759,-1.1176619927957 | |||||
| 3.1,-0.515613103962611,2.74891875894459,3.39005668287868,-0.332357611269986 | |||||
| 3.2,-0.226326357533143,3.01046279160286,1.78219595985548,0.466196819401975 | |||||
| 3.3,0.0807823484948785,3.10169417161173,0.0444195098736388,1.24616545405351 | |||||
| 3.4,0.388335249621637,3.01614941528424,-1.75393602905129,1.97645340455444 | |||||
| 3.5,0.678348790457882,2.7560797824945,-3.43408611860293,2.62794639487516 | |||||
| 3.6,0.934021470108098,2.33567935225527,-4.86907935984763,3.17467145539661 | |||||
| 3.7,1.14100335615984,1.78100950577136,-6.08628991994047,3.59483238324651 | |||||
| 3.8,1.28712234301217,1.12495585256584,-6.94253943286844,3.87167868812595 | |||||
| 3.9,1.36381593553582,0.406902302885183,-7.28297214851448,3.99417338149842 | |||||
| 4,1.36767980657433,-0.330174021755641,-7.26531793532952,3.95743298649353 | |||||
| 4.1,1.29889049825954,-1.04224588166547,-6.8546938160307,3.76292222671909 | |||||
| 4.2,1.16155425178444,-1.68650054567169,-5.94967344220412,3.41839563235312 | |||||
| 4.3,0.964721270887307,-2.22697247599071,-4.74230088590455,2.93758839149645 | |||||
| 4.4,0.720465281131124,-2.63413817732492,-3.30905701113038,2.33966877156705 | |||||
| 4.5,0.443118721263638,-2.88581866922071,-1.7019965436784,1.64847394096703 | |||||
| 4.6,0.148752195959367,-2.9721968288911,-0.0363712415656969,0.891559656400984 | |||||
| 4.7,-0.145978041760561,-2.89314281403451,1.60780240616761,0.0991017018134311 | |||||
| 4.8,-0.424630255418812,-2.6573248762253,3.05425204912372,-0.697307124891926 | |||||
| 4.9,-0.672739948585826,-2.28475882540464,4.28045566687232,-1.46591651700771 | |||||
| 5,-0.878045085084117,-1.80273599561743,5.25923148399132,-2.17608444355748 | |||||
| 5.1,-1.0307579067425,-1.24353668430421,5.82481140361667,-2.79949875037417 | |||||
| 5.2,-1.12522261436471,-0.64300440916985,6.04748257510137,-3.31130587634261 | |||||
| 5.3,-1.1592124962359,-0.0379409362849631,5.93663216000362,-3.69110168645123 | |||||
| 5.4,-1.13383605650707,0.536222156936198,5.4497172587264,-3.92374492026597 | |||||
| 5.5,-1.05396244419096,1.0488134681975,4.70608941857471,-3.99996082620281 | |||||
| 5.6,-0.927027937689112,1.47376030771876,3.73555922576465,-3.91671091660527 | |||||
| 5.7,-0.762737838929616,1.79264354239405,2.61355404944882,-3.6773141026587 | |||||
| 5.8,-0.572312199675631,1.99548574983561,1.42458709467826,-3.29131437987483 | |||||
| 5.9,-0.367640689474864,2.07886112031207,0.262305797895213,-2.77410033910849 | |||||
| 6,-0.160346121295144,2.04848897718534,-0.810850096629073,-2.14629167200174 | |||||
| 6.1,0.0388399459182844,1.91690138358474,-1.7735540422846,-1.43291712894731 | |||||
| 6.2,0.220290472708867,1.70086688471167,-2.49938359217591,-0.662416701793238 | |||||
| 6.3,0.376747163577691,1.42178996137362,-2.98924153660433,0.134492188884554 | |||||
| 6.4,0.503311439080471,1.10348685128045,-3.29015849694172,0.926039300406156 | |||||
| 6.5,0.596974129613834,0.769202496718443,-3.33640210419518,1.68066814730656 | |||||
| 6.6,0.657272799105245,0.440521180295967,-3.17264695963293,2.3682940588289 | |||||
| 6.7,0.685844999000327,0.135894667251945,-2.86638329348033,2.96150355980979 | |||||
| 6.8,0.685753365960606,-0.130056648987916,-2.42584670939147,3.43664725942599 | |||||
| 6.9,0.66140326582697,-0.348319746055368,-1.9226177252087,3.77478267777642 | |||||
| 7,0.617826988441247,-0.514598278935145,-1.4050180793338,3.96242942277948 | |||||
| 7.1,0.560200530262186,-0.629615801215413,-0.916072884584706,3.99210661086545 | |||||
| 7.2,0.493413343237278,-0.698799738553371,-0.492918132824704,3.86263110619711 | |||||
| 7.3,0.421696974884123,-0.730300222058687,-0.171396746593982,3.57916468856201 | |||||
| 7.4,0.348266639065028,-0.734788651043527,0.0391562230663334,3.15300826950127 | |||||
| 7.5,0.275227865476597,-0.723747007930665,0.146209239141171,2.60115136062847 | |||||
| 7.6,0.203651184279577,-0.707781762836823,0.149580300874469,1.94559475541519 | |||||
| 7.7,0.133570306091302,-0.695777792179925,0.0729875409504171,1.21247342698281 | |||||
| 7.8,0.0642193033125308,-0.693970566176327,-0.0528266102661962,0.431014609197769 | |||||
| 7.9,-0.00565996556890208,-0.705189843622758,-0.176774620509154,-0.367627400910727 | |||||
| 8,-0.0773069806554265,-0.728754337147554,-0.272236743211374,-1.15161326666026 | |||||
| 8.1,-0.151676363174065,-0.760025340521132,-0.320431798418941,-1.88968794559386 | |||||
| 8.2,-0.229250063676892,-0.791068874381493,-0.269443420196352,-2.5524267293918 | |||||
| 8.3,-0.309518198381683,-0.812020729944363,-0.116985223730814,-3.11340831413719 | |||||
| 8.4,-0.390956185323783,-0.811937896451692,0.150000908551928,-3.55026813432602 | |||||
| 8.5,-0.470894163180363,-0.780014211551689,0.506511756278782,-3.84558996751823 | |||||
| 8.6,-0.545767023474155,-0.706877423058831,0.987756481582191,-3.98760026416638 | |||||
| 8.7,-0.610762318952125,-0.584754897081678,1.49232424767726,-3.97063752188253 | |||||
| 8.8,-0.660834371953323,-0.410270182511013,1.99274911516514,-3.7953779916725 | |||||
| 8.9,-0.690978933802869,-0.185167021665459,2.4515939666655,-3.46880871794233 | |||||
| 9,-0.69660755598576,0.0846502421423621,2.89889571627953,-3.0039489870867 | |||||
| 9.1,-0.673247221005856,0.38886209853353,3.18600736796194,-2.41933128962514 | |||||
| 9.2,-0.618026812346333,0.712716882427269,3.24837904850609,-1.73826248828757 | |||||
| 9.3,-0.530322613201749,1.03769639917485,3.14927230108926,-0.987894646946484 | |||||
| 9.4,-0.411125691046272,1.34339406863417,2.88048334532758,-0.19814256351347 | |||||
| 9.5,-0.263123935437519,1.60779762342013,2.36197978077322,0.599508838651809 | |||||
| 9.6,-0.0915023820210343,1.81056496541803,1.63746143257671,1.37325971527959 | |||||
| 9.7,0.0964937857212176,1.93408194004453,0.767273551172054,2.0922630606308 | |||||
| 9.8,0.29216268897519,1.96313670409293,-0.221801959468998,2.72785448027254 | |||||
| 9.9,0.485613572634473,1.88840380409875,-1.26370594814139,3.25469495002842 | |||||
| 10,0.666427396812341,1.70781029255568,-2.32502138310778,3.65178100291051 | |||||
| 10.1,0.823991007159132,1.42465365235776,-3.33319403023266,3.9032820710679 | |||||
| 10.2,0.948222677203596,1.04894121731209,-4.13865076550263,3.99917160057068 | |||||
| 10.3,1.03106783959303,0.598156775647966,-4.76046725558521,3.93562677847447 | |||||
| 10.4,1.06630832942662,0.0947352695087426,-5.2178509060175,3.71518093630897 | |||||
| 10.5,1.04937031020003,-0.434312443933761,-5.31641723595164,3.34662255414422 | |||||
| 10.6,0.979268118613925,-0.959752129511336,-5.08241943079766,2.84464489162393 | |||||
| 10.7,0.858341732719843,-1.45161171663342,-4.62975436959168,2.22926021407065 | |||||
| 10.8,0.691117803129844,-1.88025259648709,-3.867248155187,1.52500196661977 | |||||
| 10.9,0.485221391987975,-2.21970646439723,-2.85754093317886,0.759946703181751 | |||||
| 11,0.250749571514318,-2.44943291557137,-1.67161013024184,-0.0354052371616155 | |||||
| 11.1,-0.000438350261758313,-2.55312745846465,-0.375763795189948,-0.829345682427035 | |||||
| 11.2,-0.255383909989734,-2.52309987678432,0.952965679522388,-1.59022273248573 | |||||
| 11.3,-0.500799812922485,-2.36022031937371,2.28511009480977,-2.28770262043824 | |||||
| 11.4,-0.723364614907139,-2.07139984431106,3.47086400980713,-2.89397902417698 | |||||
| 11.5,-0.911220776793722,-1.6717298045001,4.42872084424201,-3.38488161670068 | |||||
| 11.6,-1.05478973023788,-1.18365614859635,5.21919831200576,-3.74083966077816 | |||||
| 11.7,-1.14616670056199,-0.633909431993279,5.71312747678929,-3.9476622324826 | |||||
| 11.8,-1.1804123961182,-0.0529039972742618,5.81110139261212,-3.99710396854651 | |||||
| 11.9,-1.15654707774829,0.527556150777705,5.65764025054154,-3.88719378297545 | |||||
| 12,-1.07610535687297,1.07571672648671,5.2163127831585,-3.6223134480265 | |||||
| 12.1,-0.943500508166058,1.56146712848275,4.43697105900003,-3.21302290677582 | |||||
| 12.2,-0.766525948869148,1.96035615835787,3.4609293991261,-2.6756392815121 | |||||
| 12.3,-0.554942095580977,2.25250630665306,2.3272368398947,-2.03158636156249 | |||||
| 12.4,-0.32008587389386,2.42370796171182,1.08931263730755,-1.3065405044189 | |||||
| 12.5,-0.0743365258336663,2.46879082652308,-0.1770192409213,-0.529407000391092 | |||||
| 12.6,0.169642629817314,2.38887320745735,-1.41378215966272,0.2688322901019 | |||||
| 12.7,0.399483963871667,2.19126967373951,-2.49538473357942,1.05635408553788 | |||||
| 12.8,0.604371450590226,1.89125156271722,-3.41634101074438,1.80176237710156 | |||||
| 12.9,0.775095527201341,1.50871959992942,-4.16363340087401,2.47534008848015 | |||||
| 13,0.904183269803716,1.06691912927852,-4.60578356433584,3.05023380191841 | |||||
| 13.1,0.987213176762733,0.591483046925517,-4.80212576778471,3.50352431924356 | |||||
| 13.2,1.0222218260439,0.108629047861588,-4.76881448780202,3.81714037797079 | |||||
| 13.3,1.00954233044705,-0.356205183827859,-4.45876635868854,3.97857909551135 | |||||
| 13.4,0.952275171263315,-0.780824415768228,-3.96220376540242,3.98140441964624 | |||||
| 13.5,0.855385974425555,-1.14594637692938,-3.2952486798697,3.82550371361801 | |||||
| 13.6,0.725544290789098,-1.4371149546949,-2.50230123302698,3.5170922466029 | |||||
| 13.7,0.570679594822371,-1.64564000854823,-1.64702732564788,3.06846541054212 | |||||
| 13.8,0.399344625599165,-1.76678408803482,-0.780867714276601,2.49750854166557 | |||||
| 13.9,0.220200979233193,-1.80188062145097,0.0469489535935452,1.82698388857678 | |||||
| 14,0.0415268224031566,-1.75709452297478,0.824257478983237,1.08362315323148 | |||||
| 14.1,-0.128904759637047,-1.64114478327725,1.4702707582532,0.297061782337445 | |||||
| 14.2,-0.284633634094719,-1.46622301139372,1.97079614706245,-0.501342504385716 | |||||
| 14.3,-0.420654547081767,-1.24683654154735,2.3617661103195,-1.27975984753679 | |||||
| 14.4,-0.533057798965619,-0.997314523257609,2.5931017548774,-2.00715720408228 | |||||
| 14.5,-0.619530033300698,-0.731801275213912,2.66333555853092,-2.65453553685187 | |||||
| 14.6,-0.679368912050467,-0.462916466781307,2.66219437240927,-3.19608591463845 | |||||
| 14.7,-0.712585847076143,-0.20205757711387,2.55190149362584,-3.61021843284074 | |||||
| 14.8,-0.720283767165562,0.0418838528707965,2.32163308146018,-3.88042293482874 | |||||
| 14.9,-0.704765356440378,0.263312972330474,2.07883133331249,-3.9959272197878 | |||||
| 15,-0.668458632382069,0.458661712399707,1.81834120086973,-3.95212649637145 | |||||
| 15.1,-0.613968496315063,0.62613158162342,1.53630267476219,-3.75076696120112 | |||||
| 15.2,-0.544115333500436,0.766427475271895,1.27216427812542,-3.39987618351731 | |||||
| 15.3,-0.461540527904553,0.881036343301911,1.02622940697853,-2.91344307132637 | |||||
| 15.4,-0.368703428238886,0.971781415266678,0.797298150514092,-2.31086017778294 | |||||
| 15.5,-0.267893347068078,1.04105962463048,0.592183486473996,-1.61615058129226 | |||||
| 15.6,-0.16116143103253,1.09030538050508,0.394598168220228,-0.857010161183551 | |||||
| 15.7,-0.0504835333147792,1.11987929835739,0.196387416210717,-0.0637034504004072 | |||||
| 15.8,0.0621582385650784,1.12950638006746,-0.00542612113233337,0.732142915922352 | |||||
| 15.9,0.174745749233613,1.11775704891626,-0.239453023627634,1.49880105459783 | |||||
| 16,0.284938729665871,1.08162158397329,-0.499980045730242,2.20570672496676 | |||||
| 16.1,0.390131909640826,1.01802771910313,-0.781014098836352,2.82467782872134 | |||||
| 16.2,0.487514948627418,0.92408182259519,-1.081230681301,3.33103794123112 | |||||
| 16.3,0.574085680801,0.797145817515727,-1.46172506984881,3.70460008272211 | |||||
| 16.4,0.646039162276094,0.635051860971208,-1.81897397838919,3.93047150945656 | |||||
| 16.5,0.699802903967296,0.437977095267359,-2.13057734233654,3.99964744042907 | |||||
| 16.6,0.732260872235133,0.208731503507477,-2.39893781212285,3.90937004956903 | |||||
| 16.7,0.740729462381741,-0.0478983366353404,-2.68422717530223,3.66323841156328 | |||||
| 16.8,0.722355780775327,-0.324577270594466,-2.85733049764952,3.27106501810577 | |||||
| 16.9,0.675408794192417,-0.611199331914063,-2.86159329006487,2.74848458481898 | |||||
| 17,0.599845874708859,-0.895577408933868,-2.75462306175829,2.1163307444801 | |||||
| 17.1,0.496736724607718,-1.16413733097779,-2.55068385730742,1.39980547582665 | |||||
| 17.2,0.368120735933503,-1.40174697538996,-2.16745299394969,0.62747438019364 | |||||
| 17.3,0.217830217319791,-1.59394033340686,-1.63449153404535,-0.169872138867806 | |||||
| 17.4,0.0511947833656253,-1.72774820042218,-0.990788498984157,-0.960446391815098 | |||||
| 17.5,-0.125348535578382,-1.79095853322587,-0.244208088454018,-1.7127306779846 | |||||
| 17.6,-0.304333935406929,-1.77494222941117,0.565762756929766,-2.39673379685706 | |||||
| 17.7,-0.477661707666179,-1.67577850449359,1.41246201984706,-2.98518670257967 | |||||
| 17.8,-0.636864859726958,-1.49279172650053,2.25451472115851,-3.45462963477182 | |||||
| 17.9,-0.773522864576152,-1.22990903082874,2.9824331051199,-3.78634738513984 | |||||
| 18,-0.880356538374148,-0.896795339672411,3.59912160219564,-3.96711541377246 | |||||
| 18.1,-0.951198996150186,-0.507078295983122,4.13585113634964,-3.98972706981459 | |||||
| 18.2,-0.980682942562729,-0.0782624790182752,4.41974070040262,-3.85328089789504 | |||||
| 18.3,-0.965969481971245,0.369209230986198,4.44685044666184,-3.56321657630745 | |||||
| 18.4,-0.906787516913142,0.813039716275539,4.32412725327608,-3.13109805420262 | |||||
| 18.5,-0.804364279322279,1.22992832619715,3.95418668923767,-2.574152533428 | |||||
| 18.6,-0.662399174839039,1.59732144999188,3.33450271279904,-1.91458367435366 | |||||
| 18.7,-0.487089043227809,1.89570309190105,2.56072149023441,-1.17868640600103 | |||||
| 18.8,-0.286171696714235,2.10752289091859,1.63380699481198,-0.395798630201158 | |||||
| 18.9,-0.0689162802525407,2.2197528765431,0.60117181028112,0.402868387970002 | |||||
| 19,0.154350854311965,2.22590557055069,-0.484649769110557,1.18547431483754 | |||||
| 19.1,0.372771491185364,2.12370409200131,-1.56606702536783,1.92081912175304 | |||||
| 19.2,0.575531457805086,1.91658596997832,-2.54192275532618,2.57958693177947 | |||||
| 19.3,0.752872196871545,1.61513069870749,-3.41107769073975,3.13551475119317 | |||||
| 19.4,0.896102159030608,1.23422981873053,-4.15639887813154,3.56643949216576 | |||||
| 19.5,0.997768132408354,0.792893829276582,-4.62323032183498,3.85518154513635 | |||||
| 19.6,1.05320180256775,0.313605645687501,-4.84812446443323,3.99022967563122 | |||||
| 19.7,1.06015422808282,-0.17954698751638,-4.91488492044845,3.96619994085656 | |||||
| 19.8,1.0179578043934,-0.660879466111878,-4.68136281855116,3.78405033050763 | |||||
| 19.9,0.928947752518464,-1.10636537743868,-4.16245180252246,3.45104257474272 | |||||
| 20,0.798313182618308,-1.49461244763109,0,2.9804526419174 | |||||
+ 39
- 0
Work 1/scripts/sample_data.m
View File
| @@ -0,0 +1,39 @@ | |||||
| function sample_data(t, x, Ts, A0, omega, filename) | |||||
| % SAMPLE_DATA - Resamples pendulum simulation data and exports to CSV | |||||
| % | |||||
| % Usage: | |||||
| % sample_pendulum_data(t, x, Ts, A0, omega, filename) | |||||
| % | |||||
| % Inputs: | |||||
| % t - time vector from ODE solver (e.g., from ode45) | |||||
| % x - state matrix [q(t), dq(t)] | |||||
| % Ts - sampling period (in seconds) | |||||
| % A0 - input amplitude for u(t) = A0 * sin(omega * t) | |||||
| % omega - input frequency (in rad/s) | |||||
| % filename - output CSV filename | |||||
| % Time vector for resampling | |||||
| t_sampled = t(1):Ts:t(end); | |||||
| % Resample q and dq using interpolation | |||||
| q_sampled = interp1(t, x(:,1), t_sampled); | |||||
| dq_sampled = interp1(t, x(:,2), t_sampled); | |||||
| % Estimate second derivative using central finite differences | |||||
| ddq_sampled = zeros(size(q_sampled)); | |||||
| N = length(q_sampled); | |||||
| for k = 2:N-1 | |||||
| ddq_sampled(k) = (q_sampled(k+1) - 2*q_sampled(k) + q_sampled(k-1)) / Ts^2; | |||||
| end | |||||
| % Evaluate input u(t) | |||||
| u_sampled = A0 * sin(omega * t_sampled); | |||||
| % Create table and export to CSV | |||||
| T = table(t_sampled', q_sampled', dq_sampled', ddq_sampled', u_sampled', ... | |||||
| 'VariableNames', {'t', 'q', 'dq', 'ddq', 'u'}); | |||||
| writetable(T, filename); | |||||
| fprintf('Sampling data saved to file: %s\n', filename); | |||||
| end | |||||