21 измењених фајлова са 137 додато и 55 уклоњено
+ 1
- 1
.gitignore
Прегледај датотеку
BIN
Work 3/report/Work3_report.pdf
Прегледај датотеку
+ 117
- 13
Work 3/report/Work3_report.tex
Прегледај датотеку
+ 0
- 33
Work 3/scripts/GivenEnv.asv
Прегледај датотеку
+ 15
- 4
Work 3/scripts/Script_1_SteepDesc.m
Прегледај датотеку
+ 1
- 1
Work 3/scripts/Script_2_SteepDesc_Proj.m
Прегледај датотеку
+ 2
- 2
Work 3/scripts/Script_3_SteepDesc_Proj.m
Прегледај датотеку
+ 1
- 1
Work 3/scripts/Script_4_SteepDesc_Proj.m
Прегледај датотеку
BIN
Work 3/scripts/figures/Plot_Contour.png
Прегледај датотеку
BIN
Work 3/scripts/figures/Plot_Function.png
Прегледај датотеку
BIN
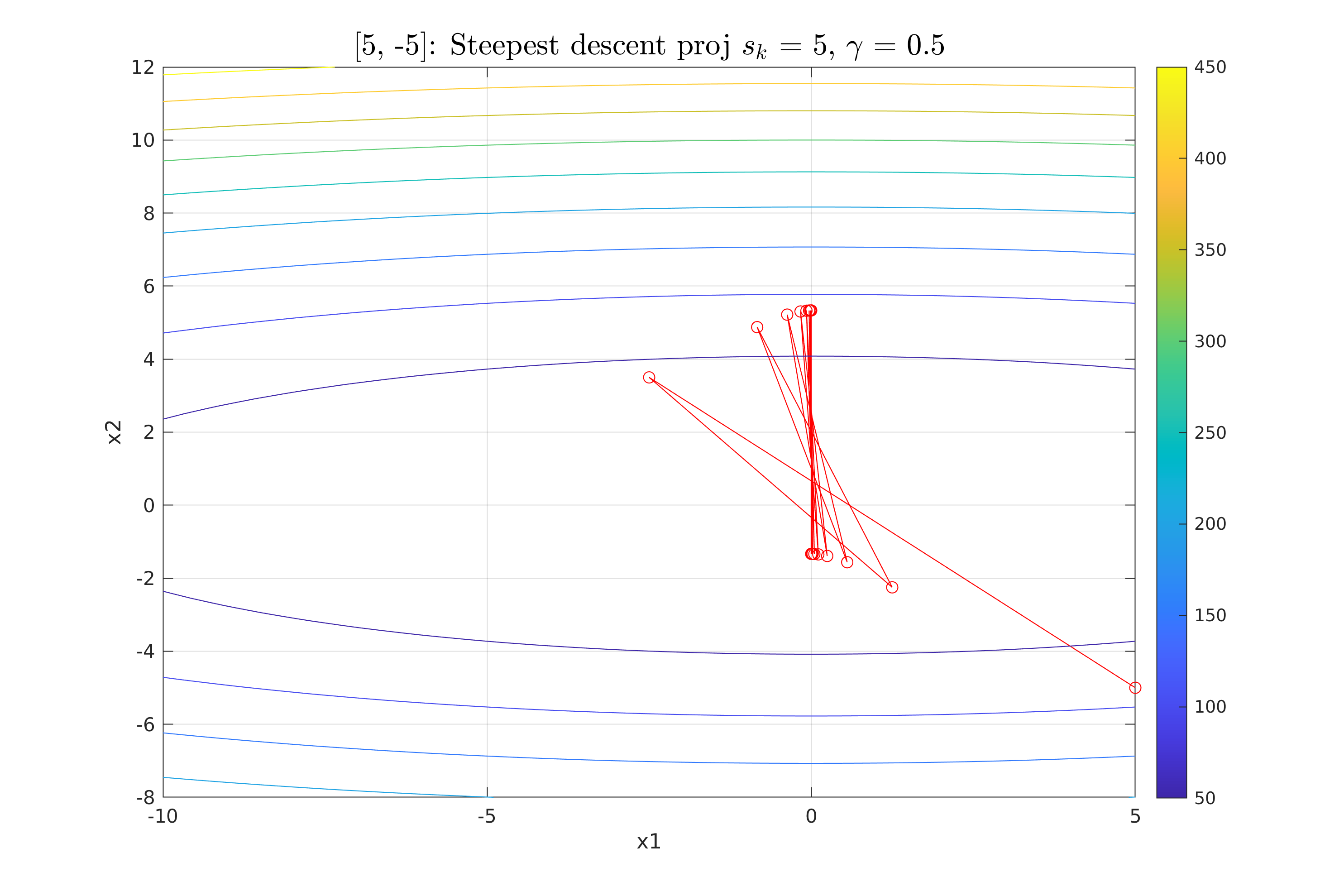
Work 3/scripts/figures/StDesProj_gamma_0.5_sk_5.png
Прегледај датотеку
BIN
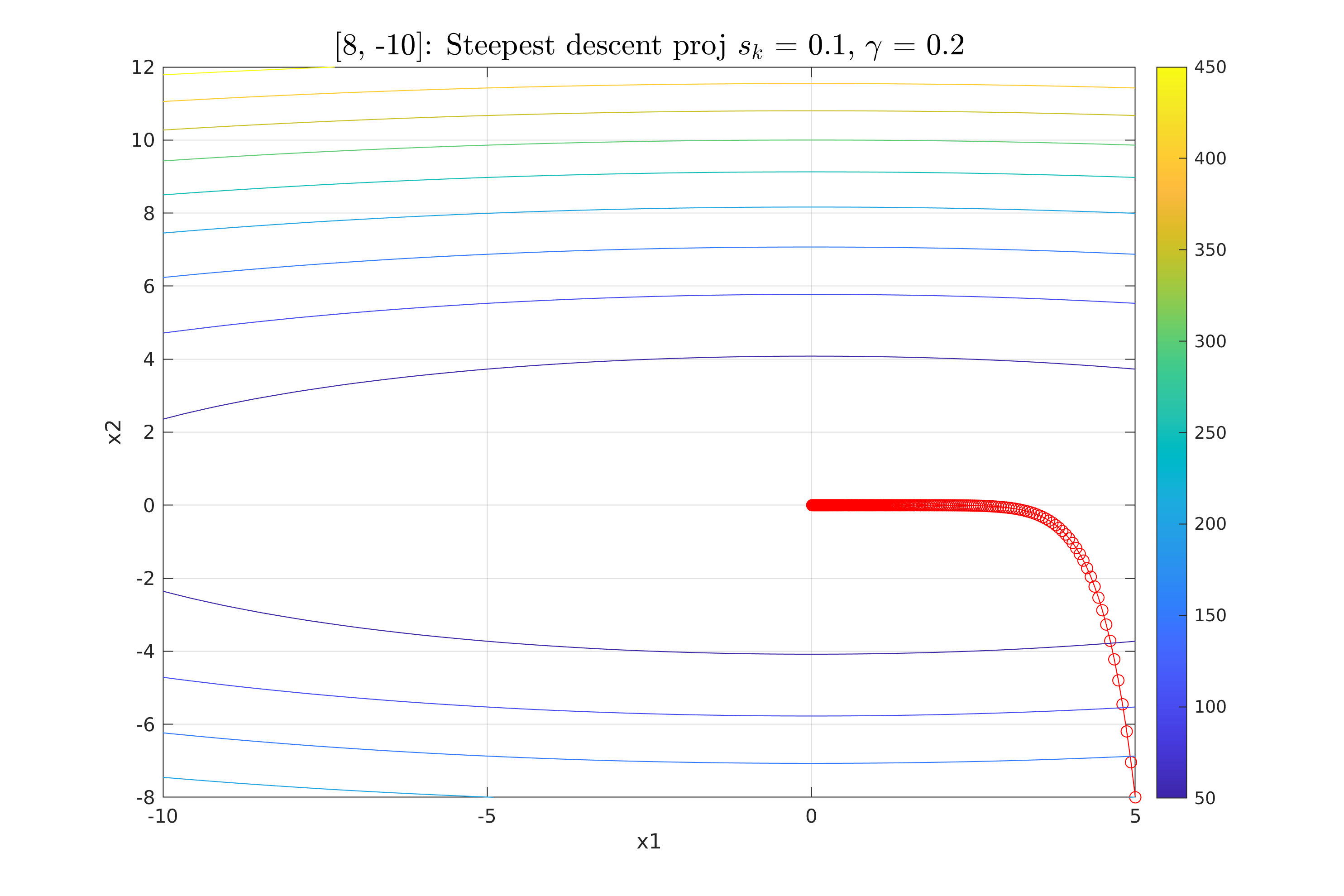
Work 3/scripts/figures/StDesProj_sk_0.1_gamma_0.2.png
Прегледај датотеку
BIN
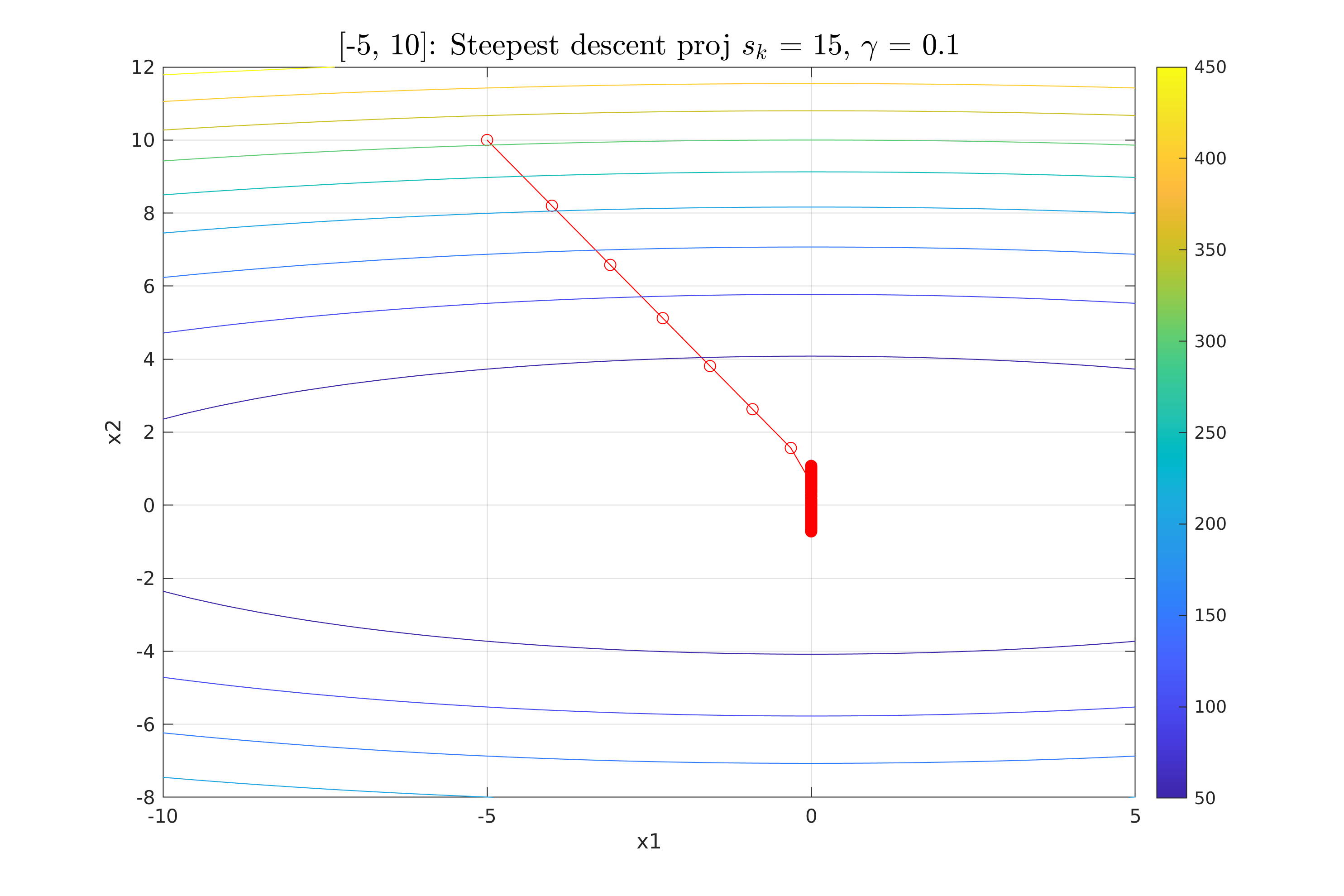
Work 3/scripts/figures/StDesProj_sk_15_gamma_0.1.png
Прегледај датотеку
BIN
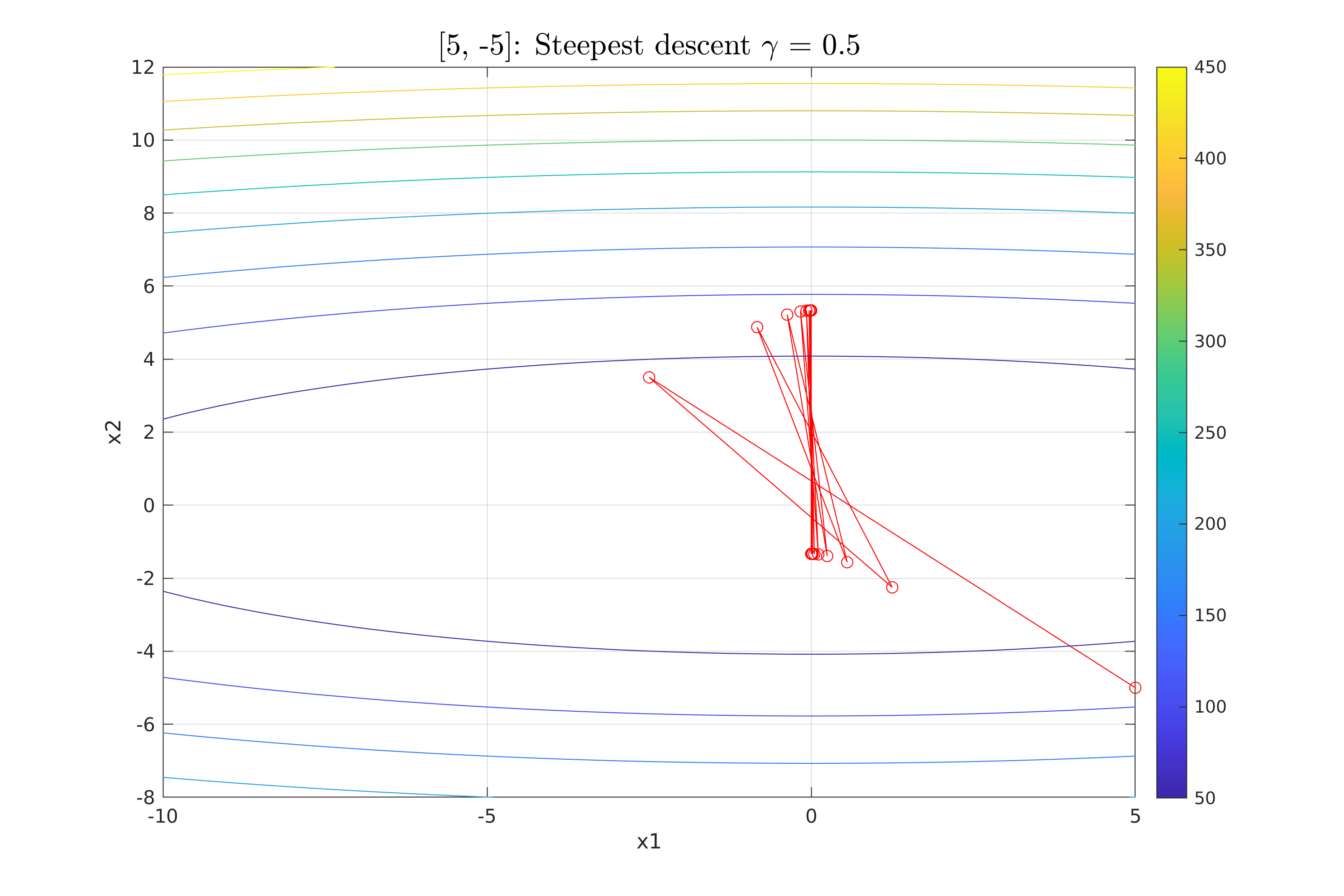
Work 3/scripts/figures/StDesProj_sk_5_gamma_0.5.png
Прегледај датотеку
BIN
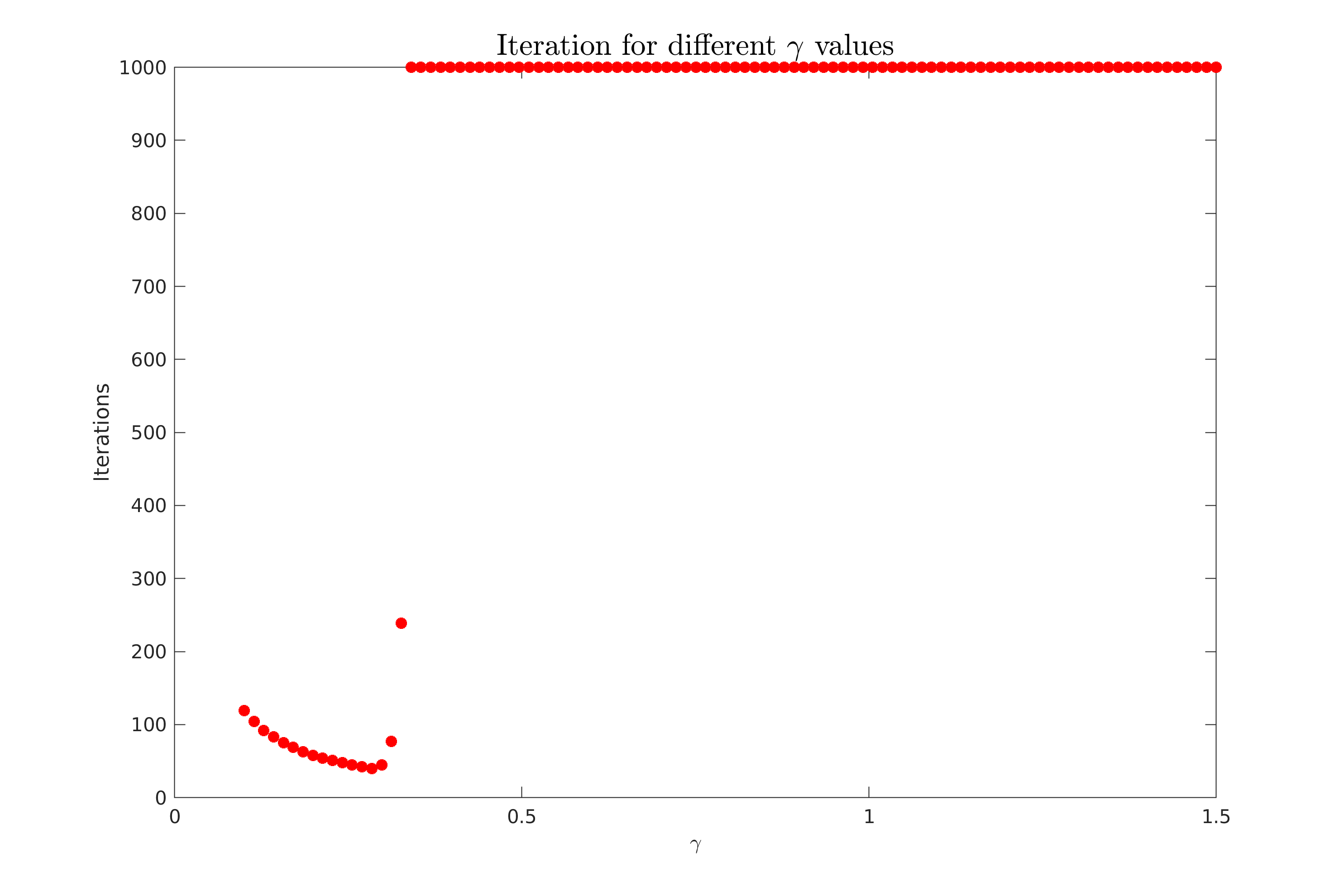
Work 3/scripts/figures/StDes_Iter_o_gamma_1.png
Прегледај датотеку
BIN
Work 3/scripts/figures/StDes_fixed_1.png
Прегледај датотеку
BIN
Work 3/scripts/figures/StDes_fixed_2.png
Прегледај датотеку
BIN
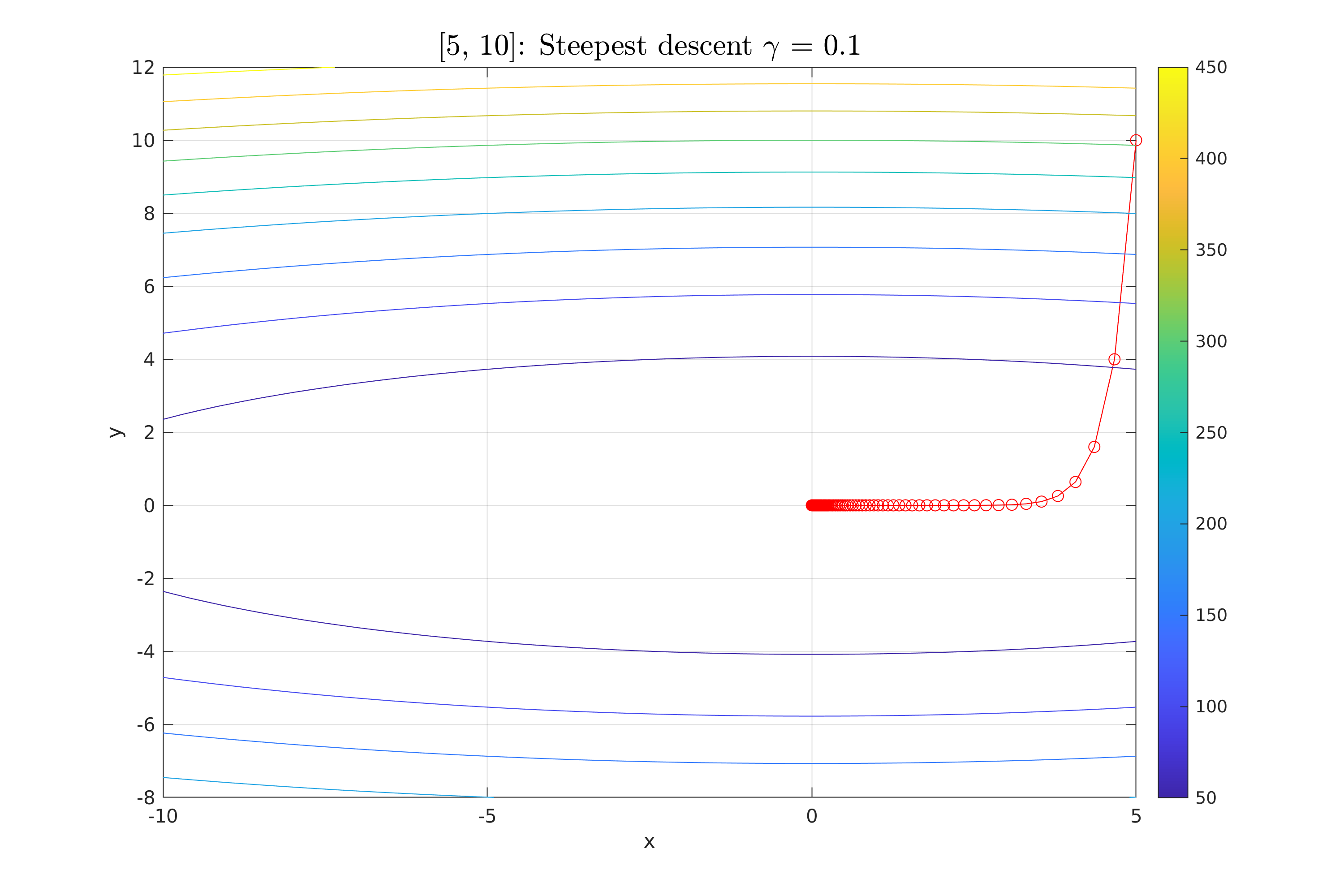
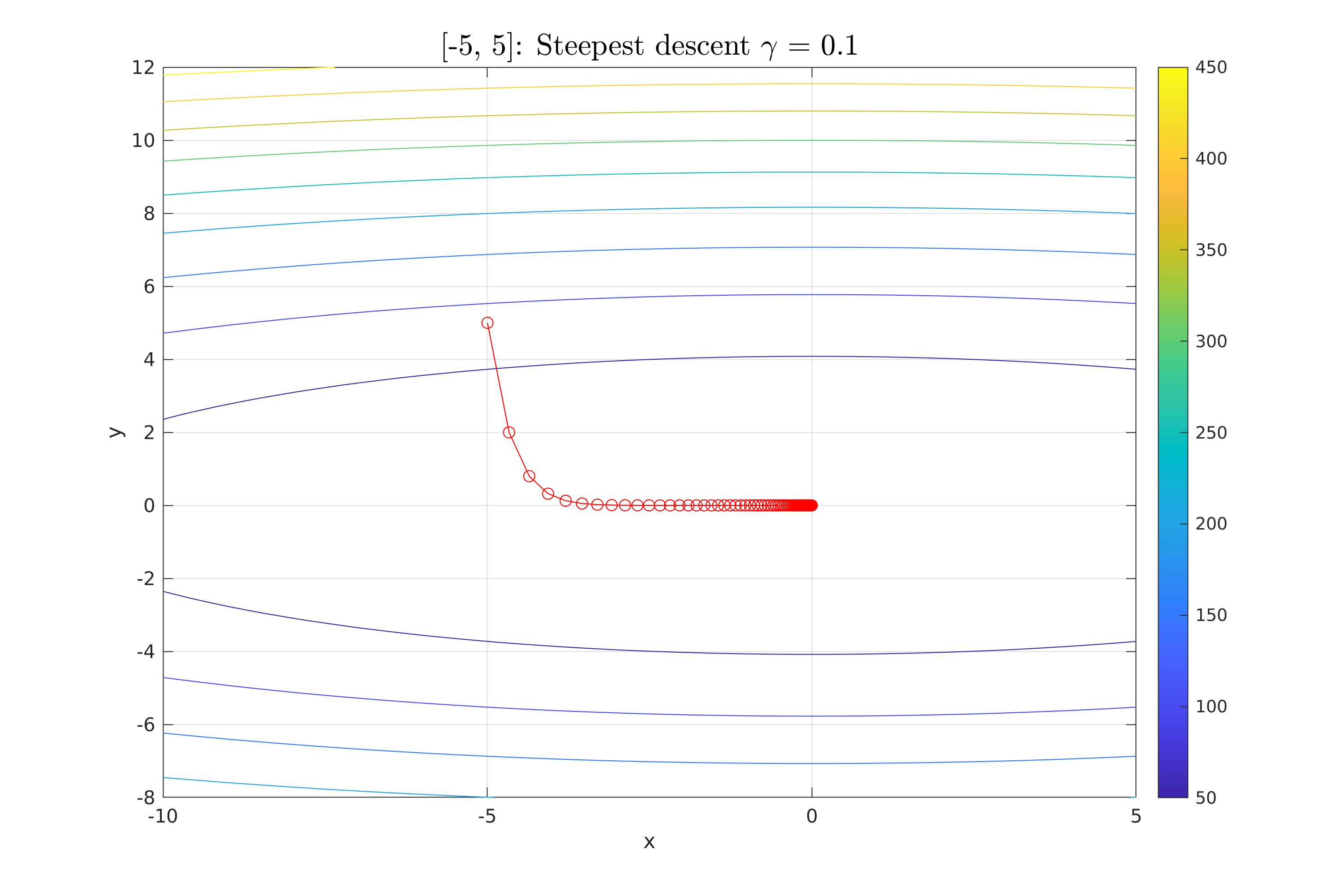
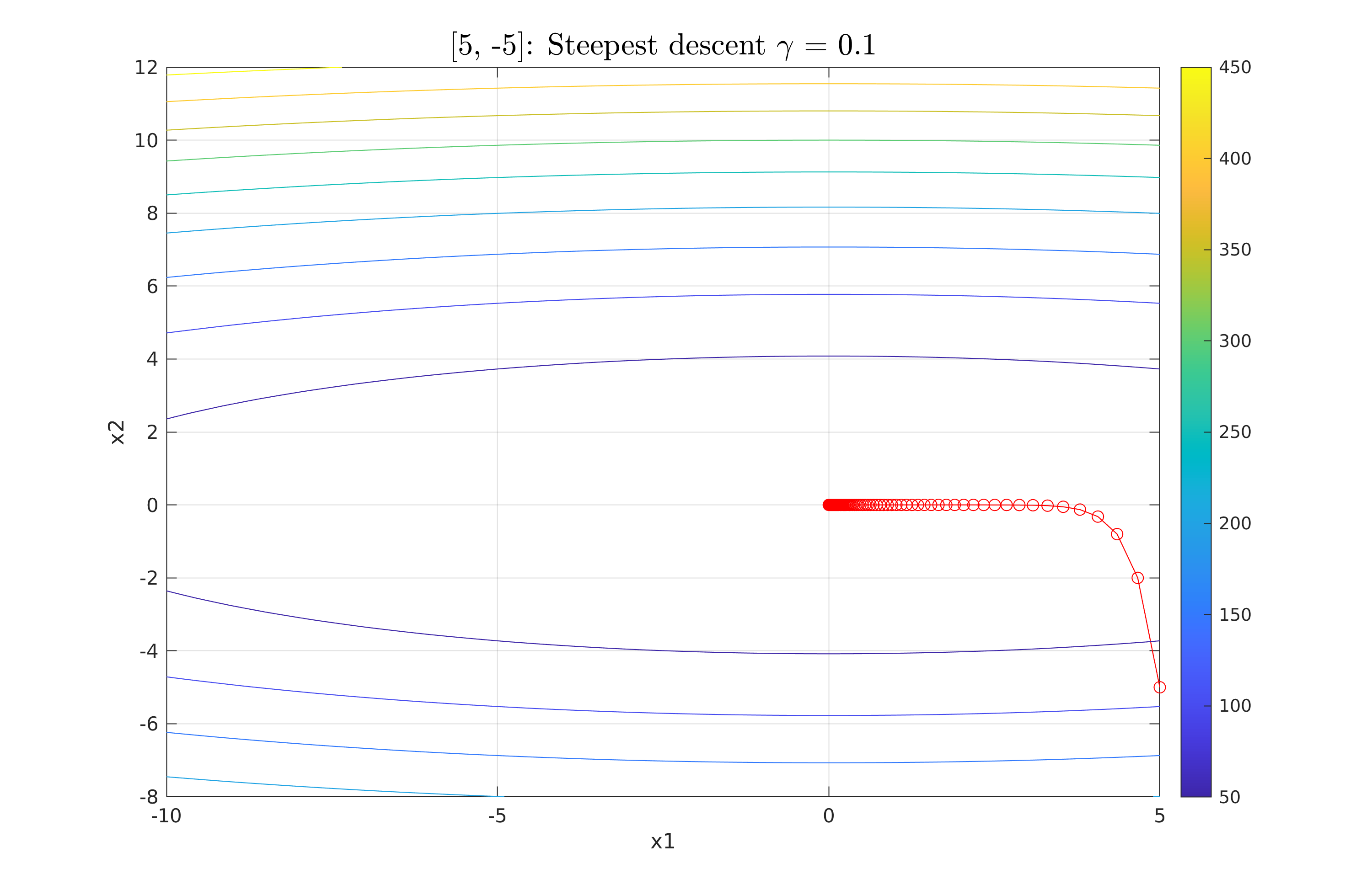
Work 3/scripts/figures/StDes_gamma_0.1.png
Прегледај датотеку
BIN
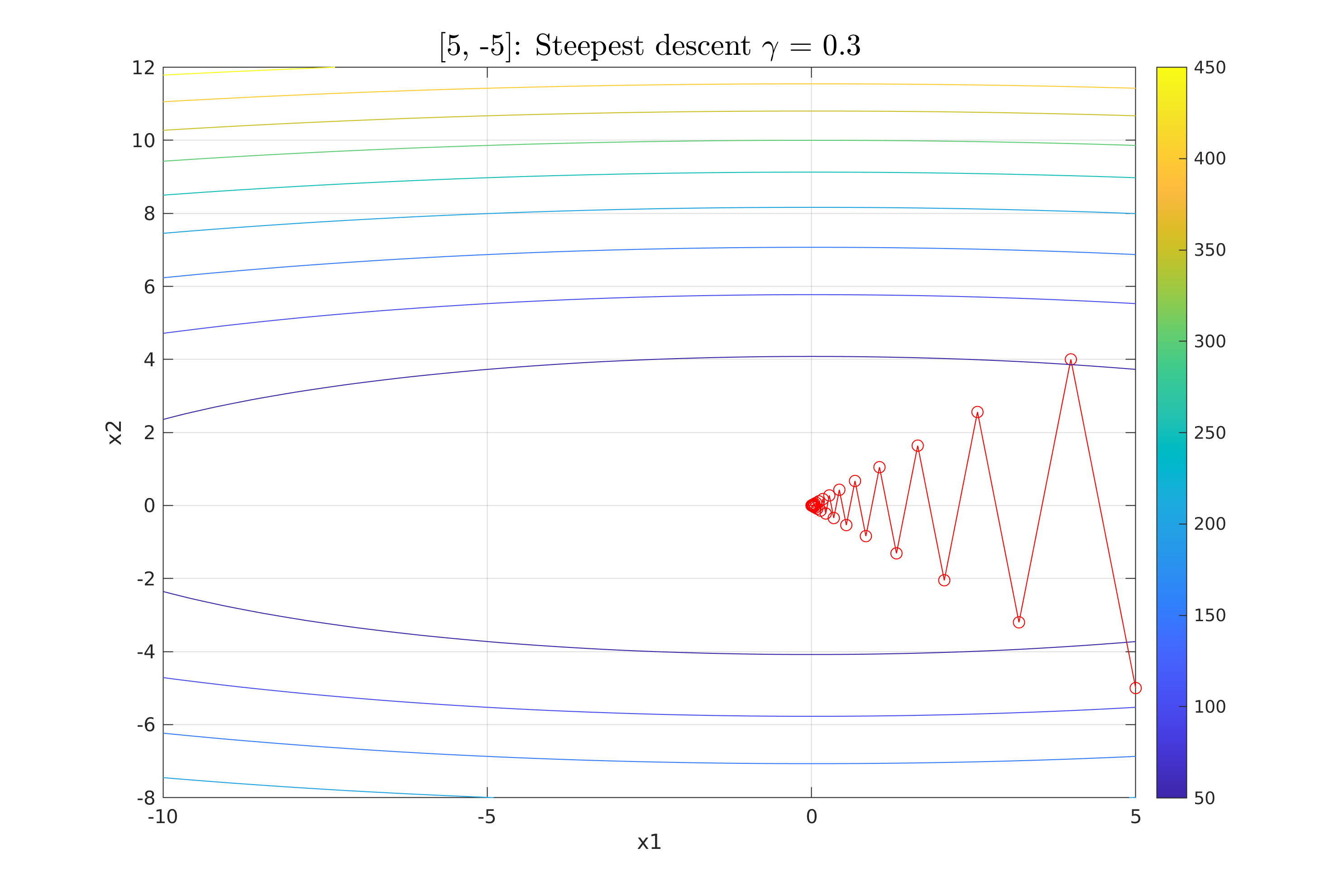
Work 3/scripts/figures/StDes_gamma_0.3.png
Прегледај датотеку
BIN
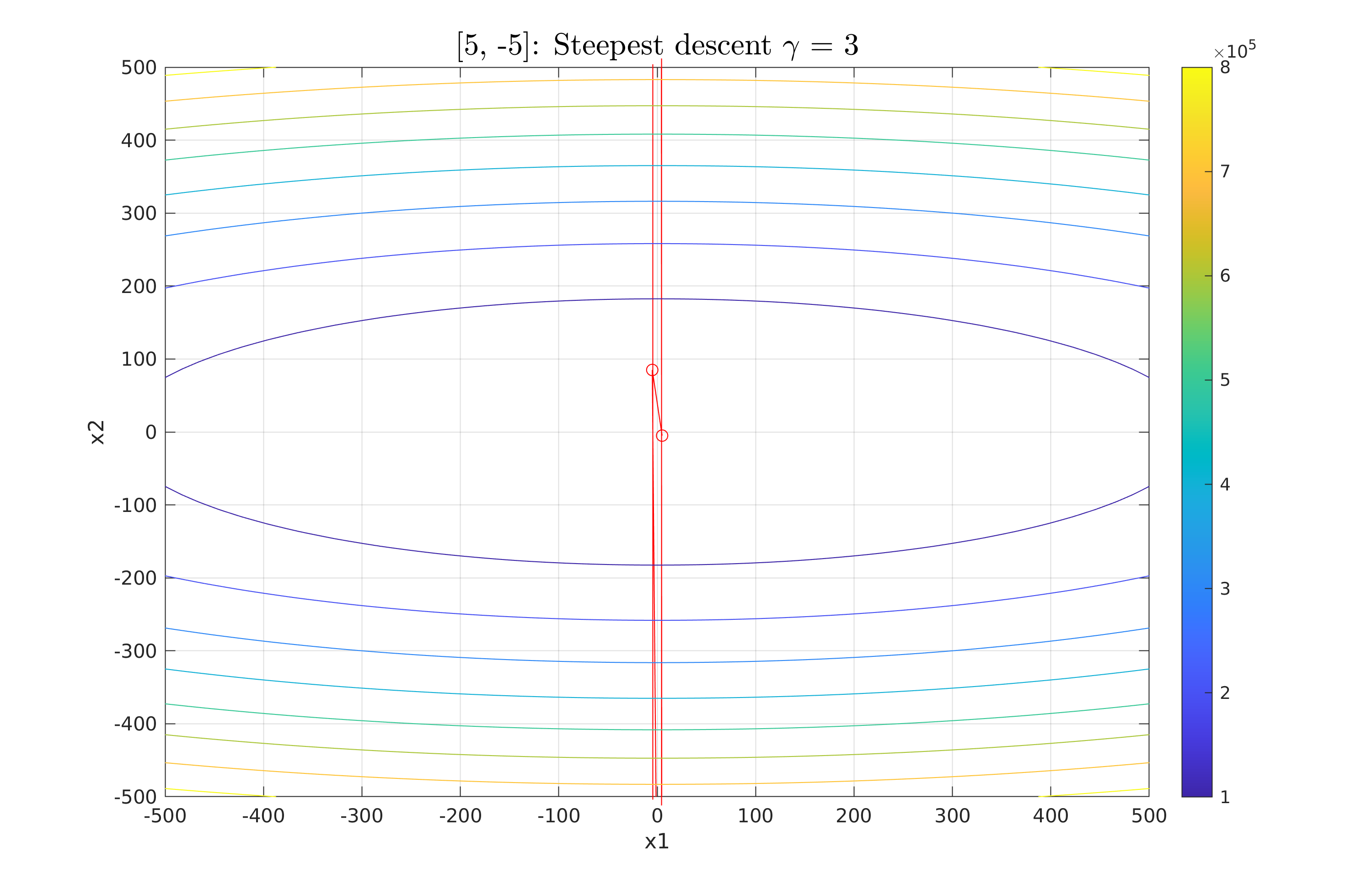
Work 3/scripts/figures/StDes_gamma_3.png
Прегледај датотеку
BIN
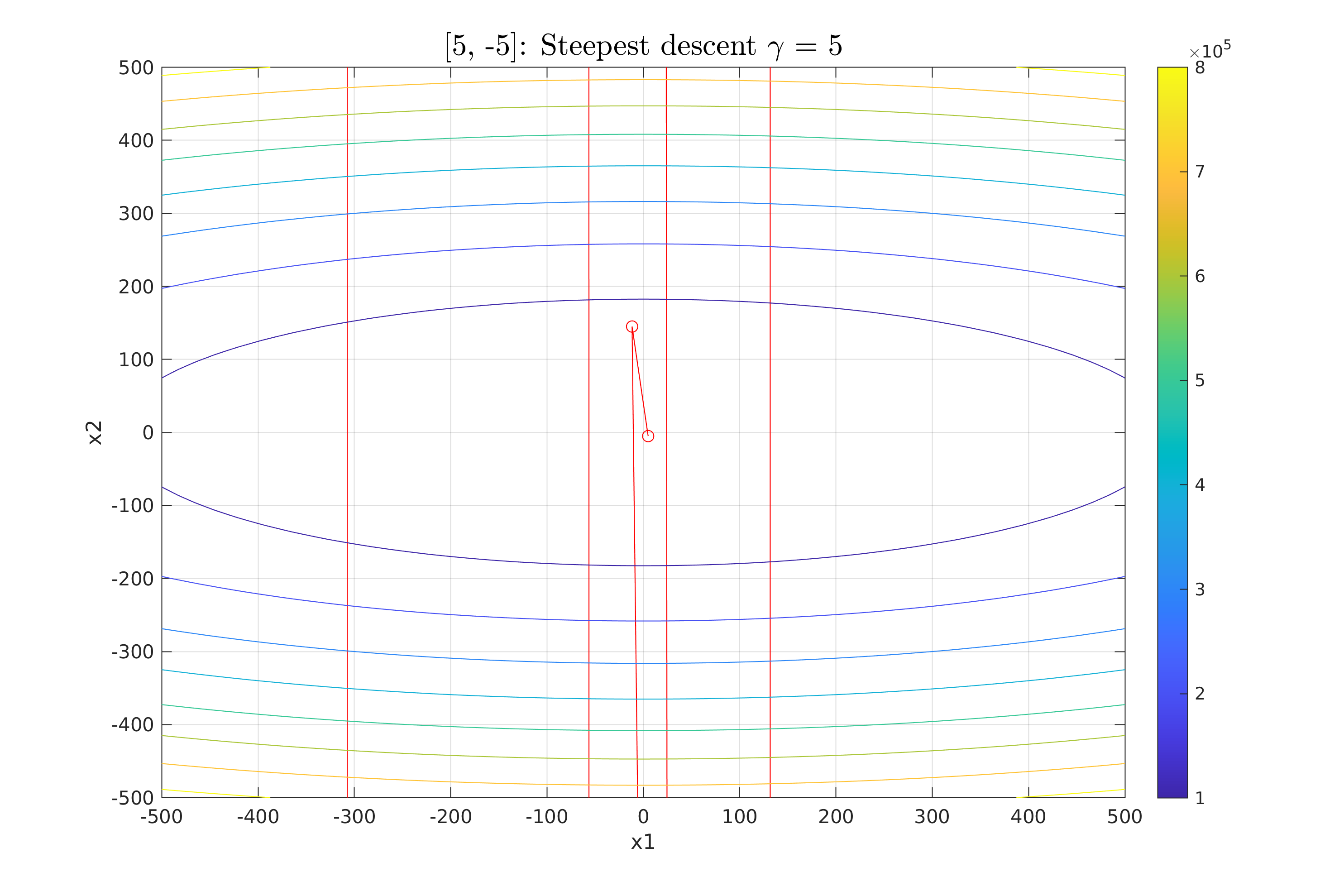
Work 3/scripts/figures/StDes_gamma_5.png
Прегледај датотеку
x
Loading…