27 changed files with 747 additions and 0 deletions
Unified View
Diff Options
-
BINWork 3/report/Work3_report.pdf
-
+93 -0Work 3/report/Work3_report.tex
-
+19 -0Work 3/scripts/BelongsTo.m
-
+33 -0Work 3/scripts/GivenEnv.asv
-
+36 -0Work 3/scripts/GivenEnv.m
-
+18 -0Work 3/scripts/ProjectionPoint.m
-
+14 -0Work 3/scripts/Script_0_Plots.m
-
+29 -0Work 3/scripts/Script_1_SteepDesc.m
-
+32 -0Work 3/scripts/Script_2_SteepDesc_Proj.m
-
+27 -0Work 3/scripts/Script_3_SteepDesc_Proj.m
-
+27 -0Work 3/scripts/Script_4_SteepDesc_Proj.m
-
BINWork 3/scripts/figures/Plot_Contour.png
-
BINWork 3/scripts/figures/Plot_Function.png
-
BINWork 3/scripts/figures/StDes_fixed_1.png
-
BINWork 3/scripts/figures/StDes_fixed_2.png
-
+49 -0Work 3/scripts/fmin_bisection.m
-
+32 -0Work 3/scripts/gamma_armijo.m
-
+12 -0Work 3/scripts/gamma_fixed.m
-
+24 -0Work 3/scripts/gamma_minimized.m
-
+39 -0Work 3/scripts/method_SteepDesc.m
-
+50 -0Work 3/scripts/method_SteepDesc_Proj.m
-
+42 -0Work 3/scripts/plot3dFun.m
-
+41 -0Work 3/scripts/plotContour.m
-
+54 -0Work 3/scripts/plotConvCompare.m
-
+28 -0Work 3/scripts/plotItersOverGamma.m
-
+48 -0Work 3/scripts/plotPointsOverContour.m
-
BINWork 3/Εργασία3.pdf
BIN
Work 3/report/Work3_report.pdf
View File
+ 93
- 0
Work 3/report/Work3_report.tex
View File
| @@ -0,0 +1,93 @@ | |||||
| % | |||||
| % Optimization Techniques Work 3 report | |||||
| % | |||||
| % authors: | |||||
| % Χρήστος Χουτουρίδης ΑΕΜ 8997 | |||||
| % cchoutou@ece.auth.gr | |||||
| \documentclass[a4paper, 11pt]{AUTHReport} | |||||
| % Document configuration | |||||
| \AuthorName{Χρήστος Χουτουρίδης} | |||||
| \AuthorAEM{8997} | |||||
| \AuthorMail{cchoutou@ece.auth.gr} | |||||
| %\CoAuthorName{CoAuthor Name} | |||||
| %\CoAuthorAEM{AEM} | |||||
| %\CoAuthorMail{CoAuthor Mail} | |||||
| % \WorkGroup{Ομάδα Χ} | |||||
| \DocTitle{3η Εργαστηριακή Άσκηση} | |||||
| \DocSubTitle{Μέθοδος Μέγιστης Καθόδου με Προβολή} | |||||
| \Department{Τμήμα ΗΜΜΥ. Τομέας Ηλεκτρονικής} | |||||
| \ClassName{Τεχνικές Βελτιστοποίησης} | |||||
| \InstructorName{Γ. Ροβιθάκης} | |||||
| \InstructorMail{rovithak@auth.gr} | |||||
| \CoInstructorName{Θ. Αφορόζη} | |||||
| \CoInstructorMail{taforozi@ece.auth.gr} | |||||
| \CurrentDate{\today} | |||||
| \usepackage{enumitem} | |||||
| \usepackage{tabularx} | |||||
| \usepackage{array} | |||||
| \usepackage{amssymb} | |||||
| \usepackage{amsfonts} | |||||
| \usepackage{amsmath} | |||||
| \usepackage{commath} | |||||
| \usepackage{float} | |||||
| \begin{document} | |||||
| \InsertTitle | |||||
| %\tableofcontents | |||||
| \sloppy | |||||
| \section{Εισαγωγή} | |||||
| Η παρούσα εργασία αφορά το πρόβλημα της ελαχιστοποίησης μιας δοσμένης συνάρτησης πολλών μεταβλητών $f: \mathbb{R}^n \rightarrow \mathbb{R}$ χωρίς περιορισμούς. | |||||
| Για το σκοπό αυτό κάνουμε χρήση τριών μεθόδων. | |||||
| Της μεθόδου μέγιστης καθόδου (Steepest Descent), της μεθόδου Newton, και της Levenberg-Marquardt. | |||||
| Ακόμα για κάθε μία από αυτές θα υλοποιήσουμε τρεις διαφορετικές τεχνικές υπολογισμού βήματος. | |||||
| \section{Παραδοτέα} | |||||
| Τα παραδοτέα της εργασίας αποτελούνται από: | |||||
| \begin{itemize} | |||||
| \item Την παρούσα αναφορά. | |||||
| \item Τον κατάλογο \textbf{scripts/}, που περιέχει τον κώδικα της MATLAB. | |||||
| \item Το \href{https://git.hoo2.net/hoo2/OptimizationTechniques/src/branch/master/Work%203}{σύνδεσμο} με το αποθετήριο που περιέχει όλο το project με τον κώδικα της MATLAB, της αναφοράς και τα παραδοτέα. | |||||
| \end{itemize} | |||||
| \section{Προγραμματιστική προσέγγιση} | |||||
| Για τον προγραμματισμό και εκτέλεση των μεθόδων της παρούσας εργασίας έγινε χρήση της MATLAB. | |||||
| Στον κατάλογο \textbf{scripts}, περιέχονται όλες οι μέθοδοι και οι τεχνικές υπολογισμού βημάτων με τη μορφή συναρτήσεων καθώς και scripts που τις καλούν. | |||||
| Για κάθε μία μέθοδο (ένα θέμα της εργασίας), υπάρχει το αντίστοιχο script που περιέχει τους υπολογισμούς, τις κλήσεις των μεθόδων και τη δημιουργία των διαγραμμάτων. | |||||
| Για το πρώτο θέμα το αρχείο Script\_1\_Plots.m για το δεύτερο το Script\_2\_Steepest\_descent.m και ούτω καθεξής. | |||||
| Στην παρούσα εργασία η υλοποίηση του κώδικα ακολουθεί την τεχνική της προηγούμενης εργασίας και “ομαδοποιεί” αρκετές λειτουργίες. | |||||
| Πιο συγκεκριμένα. | |||||
| \subsection{Symbolic expression functions} | |||||
| Μία ακόμη προγραμματιστική τεχνική που ακολουθήθηκε είναι η χρήση \textbf{symbolic expression} για την αναπαράσταση των διαφορετικών αντικειμενικών συναρτήσεων. | |||||
| Ο λόγος που επιλέχθηκε είναι η \textbf{δυνατότητα εξαγωγής ενός symbolic expression που αναπαριστά την κλίση $\nabla f$ και τον Εσσιανό $\nabla^2f$ μιας συνάρτησης} από την MATLAB, κάνοντας χρήση των εντολών \textit{gradient()} και \textit{hessian()}. | |||||
| Αν αντίθετα χρησιμοποιούσαμε απλές συναρτήσεις, πολυώνυμα ή lambdas για την αναπαράσταση των αντικειμενικών συναρτήσεων, τότε για τον υπολογισμό της κλίσης και του Εσσιανού θα έπρεπε: | |||||
| \begin{itemize} | |||||
| \item Είτε να υπολογίζαμε αριθμητικά τις παραγώγους gradient και hessian μέσα στις μεθόδους, κάτι που θα εισήγαγε \textit{\textbf{αχρείαστο αριθμητικό σφάλμα}}. | |||||
| \item Είτε να κάναμε χρήση δύο επιπλέων συναρτήσεων (ή πολυωνύμων) για την αναπαράσταση τους, κάτι που ουσιαστικά θα δημιουργούσε \textit{\textbf{πλεονασμό πληροφορίας εισόδου}} και άρα μεγαλύτερη πιθανότητα να κάνουμε λάθος. | |||||
| \end{itemize} | |||||
| Η αναπαράσταση όμως με χρήση symbolic expression είναι πιο “βαριά” όταν χρειάζεται να υπολογίσουμε την τιμή μιας συνάρτησης σε κάποιο σημείο (subs(expr, number)). | |||||
| Αυτό είναι κάτι που χρειάζεται εκτενώς στον κώδικά μας. | |||||
| Για το λόγο αυτό, ενώ η συνάρτηση δίνεται ως symbolic expression, μέσω αυτής υπολογίζονται αυτόματα η κλίση, ο Εσσιανός αλλά και οι “κανονικές” συναρτήσεις MATLAB που τις υλοποιούν. | |||||
| Έτσι έχουμε την ακριβή αναπαράσταση της κλίσης και του Εσσιανού ως συναρτήσεις χωρίς να πληρώνουμε το κόστος της subs(). | |||||
| \end{document} | |||||
+ 19
- 0
Work 3/scripts/BelongsTo.m
View File
| @@ -0,0 +1,19 @@ | |||||
| function [flag] = BelongsTo(x, SetLimmits) | |||||
| %Checks if the x vector belongs to Set | |||||
| % | |||||
| % x: A vector to project | |||||
| % SetLimmits: The set to project. Each line/dimension off the set has to contain the limits | |||||
| % of the set to that particular dimension | |||||
| % flag: True if belongs | |||||
| % | |||||
| flag = true; % Have faith | |||||
| for i = 1:size(SetLimmits, 2) | |||||
| if x(i) < SetLimmits(i,1) | |||||
| flag = false; | |||||
| elseif x(i) > SetLimmits(i,2) | |||||
| flag = false; | |||||
| end | |||||
| end | |||||
| end | |||||
+ 33
- 0
Work 3/scripts/GivenEnv.asv
View File
| @@ -0,0 +1,33 @@ | |||||
| % Given environment | |||||
| clear; | |||||
| % Setup the function under test | |||||
| syms x [2 1] real; | |||||
| fexpr = (1/3)*x(1)^2 +3*x(2)^2; | |||||
| title_fun = "$f(x) = frac{1}{3}{x_1}^2 + 3{x_2}^2$"; | |||||
| % Calculate the gradient and Hessian | |||||
| grad_fexpr = gradient(fexpr, x); % Gradient of f | |||||
| hessian_fexpr = hessian(fexpr, x); % Hessian of f | |||||
| % Convert symbolic expressions to MATLAB functions | |||||
| fun = matlabFunction(fexpr, 'Vars', {x}); % Function | |||||
| grad_fun = matlabFunction(grad_fexpr, 'Vars', {x}); % Gradient | |||||
| hessian_fun = matlabFunction(hessian_fexpr, 'Vars', {x}); % Hessian | |||||
| % Minimum reference | |||||
| %Freference = @(x) x(1).^5 .* exp(-x(1).^2 - x(2).^2); | |||||
| %[Xmin, Fmin] = fminsearch(Freference, [-1, -1]); | |||||
| % Amijo globals | |||||
| global amijo_beta; % Step reduction factor in [0.1, 0.5] (typical range: [0.1, 0.8]) | |||||
| global amijo_sigma; % Sufficient decrease constant in [1e-5, 0.1] (typical range: [0.01, 0.3]) | |||||
| %fixed step size globals | |||||
| global gamma_fixed_step | |||||
| global image_width, | |||||
| global image_height; | |||||
| image_width = 960; | |||||
| image_height = 640; | |||||
+ 36
- 0
Work 3/scripts/GivenEnv.m
View File
| @@ -0,0 +1,36 @@ | |||||
| % Given environment | |||||
| clear; | |||||
| % Setup the function under test | |||||
| syms x [2 1] real; | |||||
| fexpr = (1/3)*x(1)^2 +3*x(2)^2; | |||||
| title_fun = "$f(x) = \frac{1}{3}{x_1}^2 + 3{x_2}^2$"; | |||||
| XSetLimmits = [-10, 5 ; -8, 12]; | |||||
| % Calculate the gradient and Hessian | |||||
| grad_fexpr = gradient(fexpr, x); % Gradient of f | |||||
| hessian_fexpr = hessian(fexpr, x); % Hessian of f | |||||
| % Convert symbolic expressions to MATLAB functions | |||||
| fun = matlabFunction(fexpr, 'Vars', {x}); % Function | |||||
| grad_fun = matlabFunction(grad_fexpr, 'Vars', {x}); % Gradient | |||||
| hessian_fun = matlabFunction(hessian_fexpr, 'Vars', {x}); % Hessian | |||||
| % Minimum reference | |||||
| [Xmin, Fmin] = fminsearch(fun, [-1, -1]'); | |||||
| Xmin = round(Xmin, 3); | |||||
| Fmin = round(Fmin, 3); | |||||
| % Amijo globals | |||||
| global amijo_beta; % Step reduction factor in [0.1, 0.5] (typical range: [0.1, 0.8]) | |||||
| global amijo_sigma; % Sufficient decrease constant in [1e-5, 0.1] (typical range: [0.01, 0.3]) | |||||
| %fixed step size globals | |||||
| global gamma_fixed_step | |||||
| global image_width, | |||||
| global image_height; | |||||
| image_width = 960; | |||||
| image_height = 640; | |||||
+ 18
- 0
Work 3/scripts/ProjectionPoint.m
View File
| @@ -0,0 +1,18 @@ | |||||
| function [x_p] = ProjectionPoint(x, SetLimmits) | |||||
| %Project the x vector to Set, returns a point of Set close(st) to x | |||||
| % | |||||
| % x: A vector to project | |||||
| % SetLimmits: The set to project. Each line/dimension off the set has to contain the limits | |||||
| % of the set to that particular dimension | |||||
| %x_p: The projected point | |||||
| % | |||||
| x_p = x; | |||||
| for i = 1:size(SetLimmits, 2) | |||||
| if x(i) < SetLimmits(i,1) | |||||
| x_p(i) = SetLimmits(i,1); | |||||
| elseif x(i) > SetLimmits(i,2) | |||||
| x_p(i) = SetLimmits(i,2); | |||||
| end | |||||
| end | |||||
| end | |||||
+ 14
- 0
Work 3/scripts/Script_0_Plots.m
View File
| @@ -0,0 +1,14 @@ | |||||
| % Define environment (functions, gradients etc...) | |||||
| GivenEnv | |||||
| % | |||||
| % We plot the function in the domain of x,y in [-3, 3]. | |||||
| % We also plot the contour in order to get a sense of the min and maximum | |||||
| % points in the x-y plane | |||||
| % | |||||
| % 3d plot the function | |||||
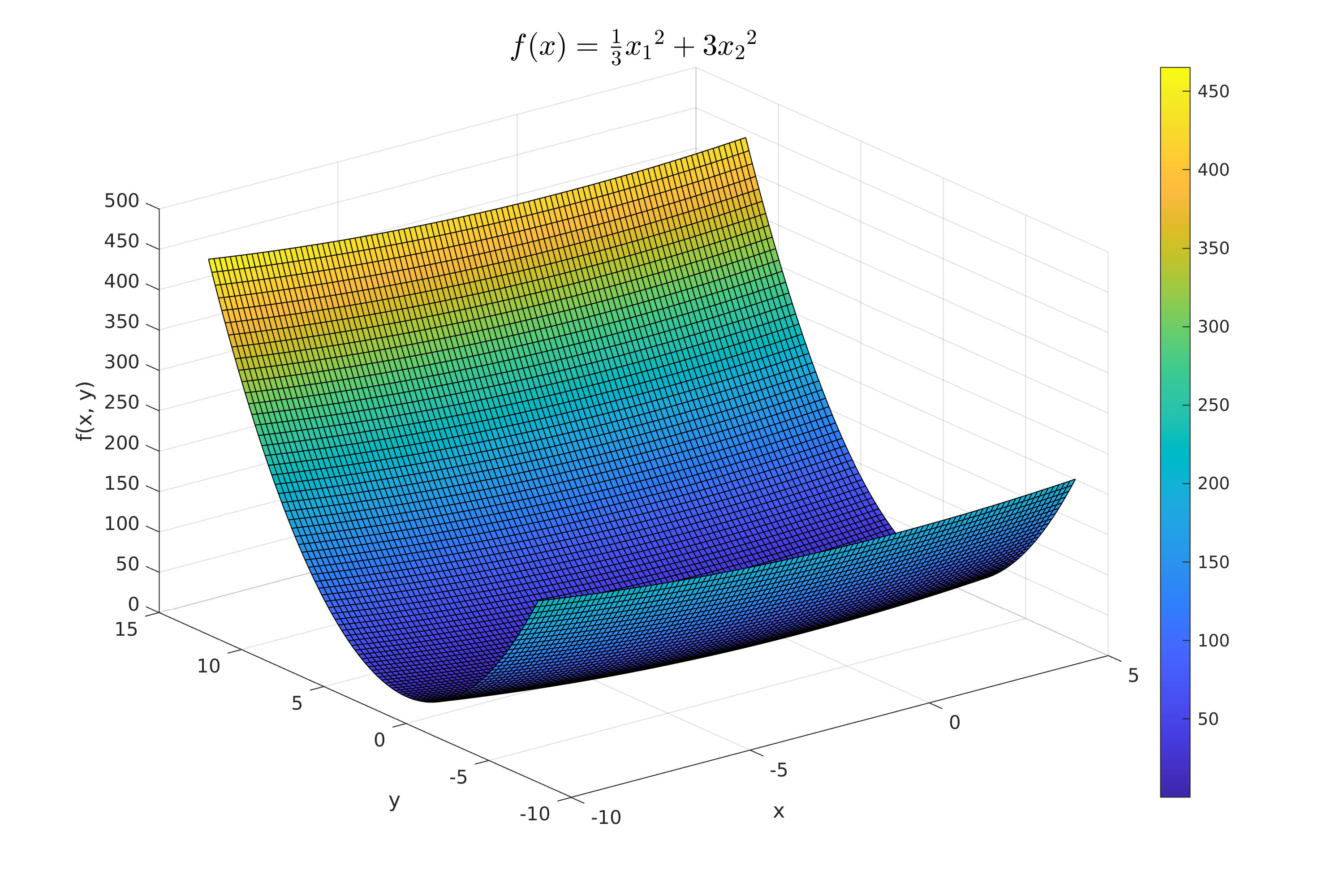
| plot3dFun(fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, title_fun, "figures/Plot_Function.png"); | |||||
| % Plot isobaric lines | |||||
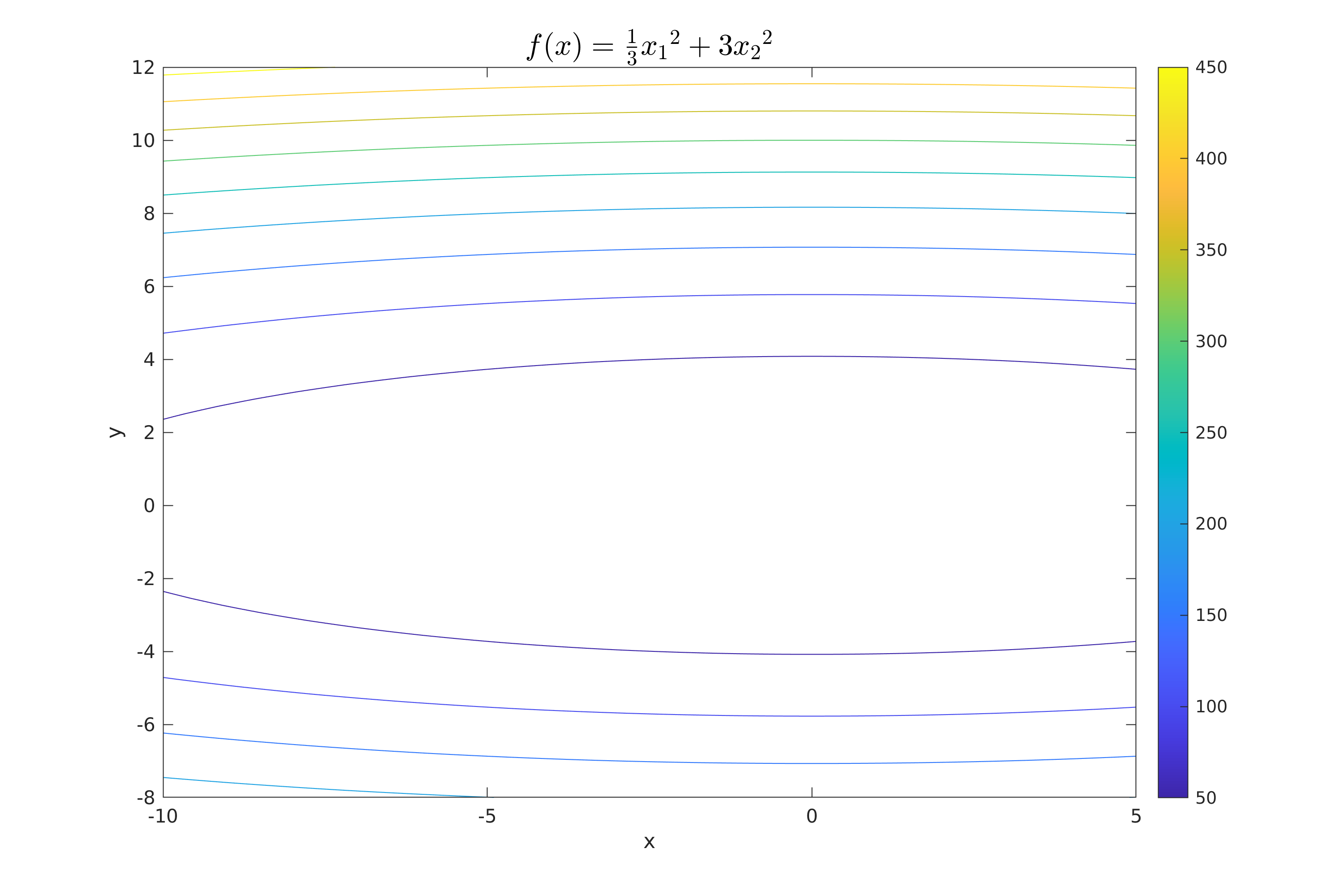
| plotContour(fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, title_fun, "figures/Plot_Contour.png"); | |||||
+ 29
- 0
Work 3/scripts/Script_1_SteepDesc.m
View File
| @@ -0,0 +1,29 @@ | |||||
| % Define environment (functions, gradients etc...) | |||||
| GivenEnv | |||||
| % Define parameters | |||||
| max_iter = 1000; % Maximum iterations | |||||
| tol = 1e-4; % Tolerance | |||||
| % Point x0 = (1, 1) | |||||
| % ========================================================================= | |||||
| point = 1; | |||||
| x0 = [5, -5]'; | |||||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||||
| f = fun(x0); | |||||
| gf = grad_fun(x0); | |||||
| hf = hessian_fun(x0); | |||||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]=> Method applicable\n', x0, f, gf, hf); | |||||
| for g=[0.1, 0.3, 0.5, 3, 5] | |||||
| gamma_fixed_step = g; | |||||
| [x_fixed, f_fixed, kk] = method_SteepDesc(fun, grad_fun, x0, tol, max_iter, 'fixed'); | |||||
| fprintf('Fixed step g=%f: Initial point (%f, %f), steps:%d, Final (x1,x2)=(%f, %f), f(x1,x2)=%f\n', g, x0, kk, x_fixed(:, end), f_fixed(end)); | |||||
| if g <= 1 | |||||
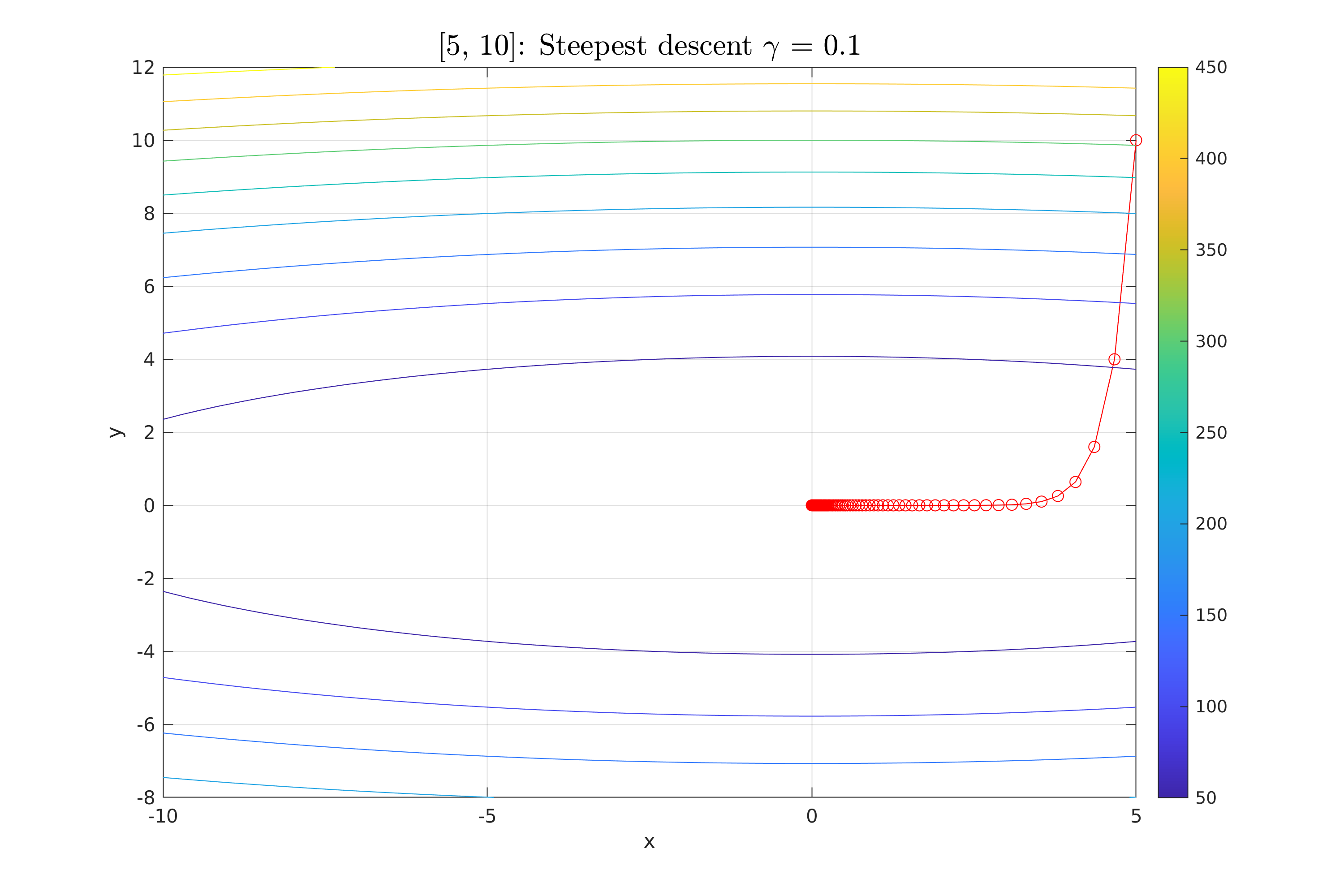
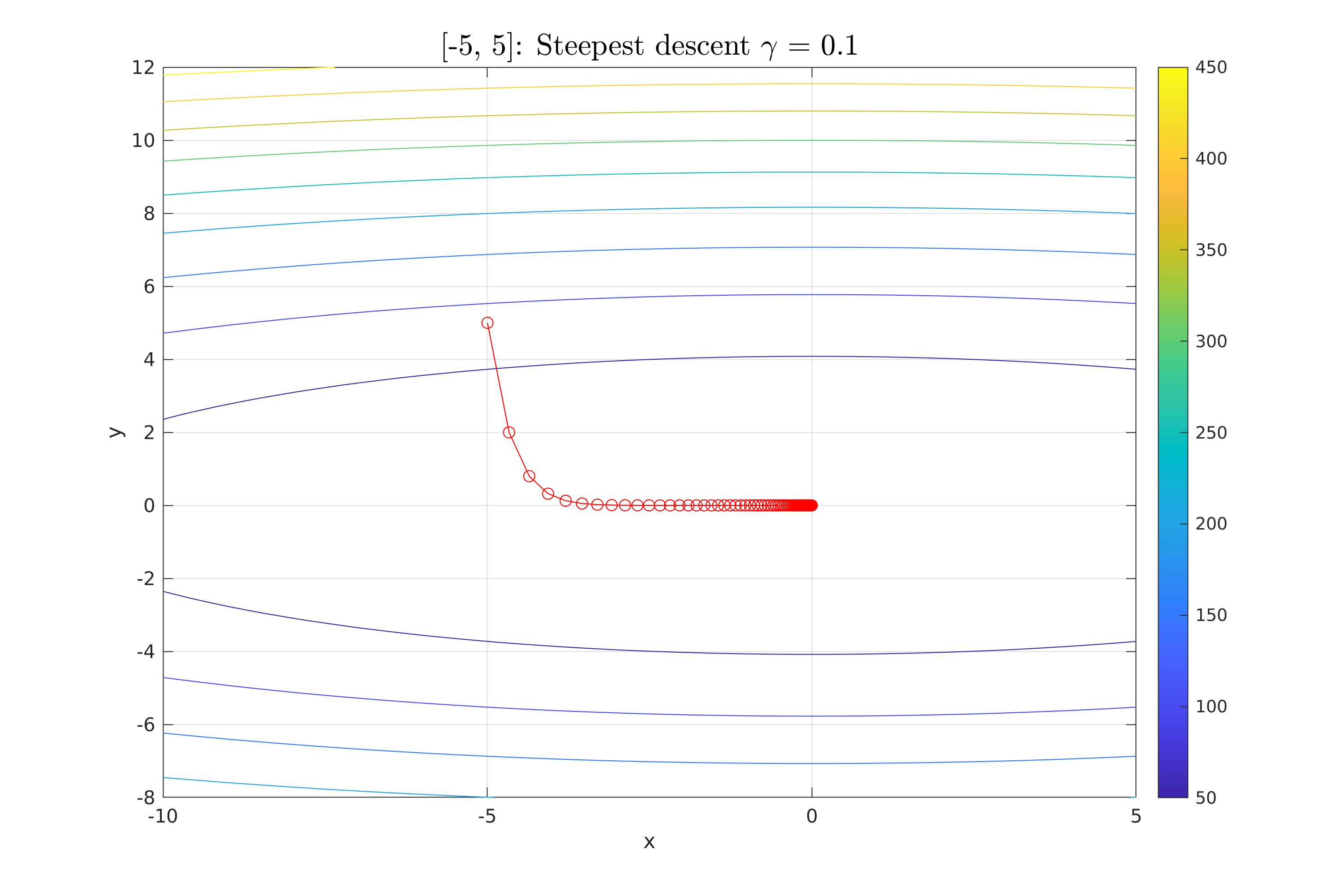
| plotPointsOverContour(x_fixed, fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, ""); | |||||
| else | |||||
| plotPointsOverContour(x_fixed, fun, [-500, 500], [-500, 500], 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, ""); | |||||
| end | |||||
| end | |||||
+ 32
- 0
Work 3/scripts/Script_2_SteepDesc_Proj.m
View File
| @@ -0,0 +1,32 @@ | |||||
| % Define environment (functions, gradients etc...) | |||||
| GivenEnv | |||||
| % Settings | |||||
| max_iter = 1000; % Maximum iterations | |||||
| % Define parameters | |||||
| % ========================================================================= | |||||
| x0 = [5, -5]'; | |||||
| gamma = 0.5; | |||||
| sk_step = 5; | |||||
| tol = 0.01; % Tolerance | |||||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||||
| f = fun(x0); | |||||
| gf = grad_fun(x0); | |||||
| hf = hessian_fun(x0); | |||||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]=> Method applicable\n', x0, f, gf, hf); | |||||
| gamma_fixed_step = gamma; | |||||
| [x_fixed, f_fixed, kk] = method_SteepDesc_Proj(fun, grad_fun, x0, sk_step, XSetLimmits, tol, max_iter, 'fixed'); | |||||
| fprintf('Fixed step g=%f: Initial point (%f, %f), steps:%d, Final (x1,x2)=(%f, %f), f(x1,x2)=%f\n', gamma_fixed_step, x0, kk, x_fixed(:, end), f_fixed(end)); | |||||
| plotPointsOverContour(x_fixed, fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, ""); | |||||
| %[x_minimized, f_minimized, kk] = method_SteepDesc_Proj(fun, grad_fun, x0, sk_step, XSetLimmits, tol, max_iter, 'minimized'); | |||||
| %fprintf('Minimized f: Initial point (%f, %f), steps:%d, Final (x1,x2)=(%f, %f), f(x1,x2)=%f\n', x0, kk, x_fixed(:, end), f_fixed(end)); | |||||
| %plotPointsOverContour(x_fixed, fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, point_str + ": Steepest descent minimized", ""); | |||||
+ 27
- 0
Work 3/scripts/Script_3_SteepDesc_Proj.m
View File
| @@ -0,0 +1,27 @@ | |||||
| % Define environment (functions, gradients etc...) | |||||
| GivenEnv | |||||
| % Settings | |||||
| max_iter = 1000; % Maximum iterations | |||||
| % Define parameters | |||||
| % ========================================================================= | |||||
| x0 = [-5, 10]'; | |||||
| gamma = 0.1; | |||||
| sk_step = 55; | |||||
| tol = 0.01; % Tolerance | |||||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||||
| f = fun(x0); | |||||
| gf = grad_fun(x0); | |||||
| hf = hessian_fun(x0); | |||||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]=> Method applicable\n', x0, f, gf, hf); | |||||
| gamma_fixed_step = gamma; | |||||
| [x_fixed, f_fixed, kk] = method_SteepDesc_Proj(fun, grad_fun, x0, sk_step, XSetLimmits, tol, max_iter, 'fixed'); | |||||
| fprintf('Fixed step g=%f: Initial point (%f, %f), steps:%d, Final (x1,x2)=(%f, %f), f(x1,x2)=%f\n', gamma_fixed_step, x0, kk, x_fixed(:, end), f_fixed(end)); | |||||
| plotPointsOverContour(x_fixed, fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, ""); | |||||
+ 27
- 0
Work 3/scripts/Script_4_SteepDesc_Proj.m
View File
| @@ -0,0 +1,27 @@ | |||||
| % Define environment (functions, gradients etc...) | |||||
| GivenEnv | |||||
| % Settings | |||||
| max_iter = 1000; % Maximum iterations | |||||
| % Define parameters | |||||
| % ========================================================================= | |||||
| x0 = [8, -10]'; | |||||
| gamma = 0.2; | |||||
| sk_step = 0.1; | |||||
| tol = 0.01; % Tolerance | |||||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||||
| f = fun(x0); | |||||
| gf = grad_fun(x0); | |||||
| hf = hessian_fun(x0); | |||||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]=> Method applicable\n', x0, f, gf, hf); | |||||
| gamma_fixed_step = gamma; | |||||
| [x_fixed, f_fixed, kk] = method_SteepDesc_Proj(fun, grad_fun, x0, sk_step, XSetLimmits, tol, max_iter, 'fixed'); | |||||
| fprintf('Fixed step g=%f: Initial point (%f, %f), steps:%d, Final (x1,x2)=(%f, %f), f(x1,x2)=%f\n', gamma_fixed_step, x0, kk, x_fixed(:, end), f_fixed(end)); | |||||
| plotPointsOverContour(x_fixed, fun, XSetLimmits(1, :), XSetLimmits(2, :), 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, ""); | |||||
BIN
Work 3/scripts/figures/Plot_Contour.png
View File
BIN
Work 3/scripts/figures/Plot_Function.png
View File
BIN
Work 3/scripts/figures/StDes_fixed_1.png
View File
BIN
Work 3/scripts/figures/StDes_fixed_2.png
View File
+ 49
- 0
Work 3/scripts/fmin_bisection.m
View File
| @@ -0,0 +1,49 @@ | |||||
| function [a, b, k, n] = fmin_bisection(fun, alpha, beta, epsilon, lambda) | |||||
| % Bisection method for finding the local minimum of a function. | |||||
| % | |||||
| % fun: The objective function | |||||
| % alpha: (number) The starting point of the interval in which we seek | |||||
| % for minimum | |||||
| % beta: (number) The ending point of the interval in which we seek | |||||
| % for minimum | |||||
| % epsilon: (number) The epsilon value (distance from midpoint) | |||||
| % lambda: (number) The lambda value (accuracy) | |||||
| % | |||||
| % return: | |||||
| % a: (vector) Starting points of the interval for each iteration | |||||
| % b: (vector) Ending points of the interval for each iteration | |||||
| % k: (number) The number of iterations | |||||
| % n: (number) The calls of objective function fun_expr | |||||
| % | |||||
| % Error checking | |||||
| if alpha > beta || 2*epsilon >= lambda || lambda <= 0 | |||||
| error ('Input criteria not met') | |||||
| end | |||||
| % Init | |||||
| a = alpha; | |||||
| b = beta; | |||||
| n = 0; | |||||
| k=1; | |||||
| while b(k) - a(k) > lambda | |||||
| % bisect [a,b] | |||||
| mid = (a(k) + b(k)) / 2; | |||||
| x_1 = mid - epsilon; | |||||
| x_2 = mid + epsilon; | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_2; | |||||
| else | |||||
| a(k) = x_1; | |||||
| b(k) = b(k-1); | |||||
| end | |||||
| end | |||||
| end | |||||
+ 32
- 0
Work 3/scripts/gamma_armijo.m
View File
| @@ -0,0 +1,32 @@ | |||||
| function [gamma] = gamma_armijo(f, grad_f, dk, xk) | |||||
| % Calculates the best step based on amijo method | |||||
| % | |||||
| % f(xk+ γk*dk) ≤ f(xk) + σ * γk * dk^T * ∇f(xk) | |||||
| % γk = β*γk_0 | |||||
| % | |||||
| % f: Objective function | |||||
| % grad_fun: Gradient function of f | |||||
| % dk: Current value of selected direction -∇f or -inv{H}*∇f or -inv{H + lI}*∇f | |||||
| % xk: Current point (x,y) | |||||
| % beta: beta factor in [0.1, 0.5] | |||||
| % signam: sigma factor in (0, 0.1] | |||||
| global amijo_beta | |||||
| global amijo_sigma | |||||
| gf = grad_f(xk); | |||||
| gamma = 1; % Start with a step size of 1 | |||||
| % Perform Armijo line search | |||||
| while f(xk + gamma * dk) > f(xk) + amijo_sigma * gamma * dk * gf | |||||
| %while f(xk(1) + gamma * dk(1), xk(2) + gamma * dk(2)) > ... | |||||
| % f(xk(1), xk(2)) + amijo_sigma * gamma * norm(dk)^2 | |||||
| gamma = amijo_beta * gamma; % Reduce step size | |||||
| if gamma < 1e-12 % Safeguard to prevent infinite reduction | |||||
| warning('Armijo step size became too small.'); | |||||
| break; | |||||
| end | |||||
| end | |||||
| end | |||||
+ 12
- 0
Work 3/scripts/gamma_fixed.m
View File
| @@ -0,0 +1,12 @@ | |||||
| function [gamma] = gamma_fixed(~, ~, ~, ~) | |||||
| % Return a fixed step | |||||
| % | |||||
| % This is for completion and code symmetry. | |||||
| % | |||||
| global gamma_fixed_step | |||||
| % Perform line search | |||||
| gamma = gamma_fixed_step; | |||||
| end | |||||
+ 24
- 0
Work 3/scripts/gamma_minimized.m
View File
| @@ -0,0 +1,24 @@ | |||||
| function [gamma] = gamma_minimized(f, ~, dk, xk) | |||||
| % Calculates the step based on minimizing f(xk− γk*dk) | |||||
| % | |||||
| % | |||||
| % f: Objective function | |||||
| % ~: Gradient function of f - Not used | |||||
| % dk: Current value of selected direction -∇f or -inv{H}*∇f or -inv{H + lI}*∇f | |||||
| % xk: Current point (x,y) | |||||
| % Define the line search function fmin(g) = f(xk - g * dk) | |||||
| fmin = @(g) f(xk) + g * dk; | |||||
| % find g that minimizes fmin | |||||
| e = 0.0001; | |||||
| l = 0.001; | |||||
| [a,b,k,~] = fmin_bisection(fmin, 0.0001, 1, e, l); % g in (0, 1] | |||||
| gamma = 0.5*(a(k) + b(k)); | |||||
| % Define the line search function fmin(g) = f(xk - g * dk) | |||||
| %fmin = @(g) f(xk(1) - gamma * dk(1), xk(2) - gamma * dk(2)); | |||||
| % find g that minimizes fmin | |||||
| %gamma = fminbnd(g, 0, 1); | |||||
| end | |||||
+ 39
- 0
Work 3/scripts/method_SteepDesc.m
View File
| @@ -0,0 +1,39 @@ | |||||
| function [x_vals, f_vals, k] = method_SteepDesc(f, grad_f, xk, tol, max_iter, mode) | |||||
| % f: Objective function | |||||
| % grad_f: Gradient of the function | |||||
| % xk: Initial point [x0; y0] | |||||
| % tol: Tolerance for stopping criterion | |||||
| % max_iter: Maximum number of iterations | |||||
| % x_vals: Vector with the (x,y) values until minimum | |||||
| % f_vals: Vector with f(x,y) values until minimum | |||||
| % k: Number of iterations | |||||
| if strcmp(mode, 'armijo') == 1 | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_armijo(f, grad_f, dk, xk); | |||||
| elseif strcmp(mode, 'minimized') == 1 | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_minimized(f, grad_f, dk, xk); | |||||
| else % mode == 'fixed' | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_fixed(f, grad_f, dk, xk); | |||||
| end | |||||
| % Storage for iterations, begin with the first point | |||||
| x_vals = xk; | |||||
| f_vals = f(xk); | |||||
| for k = 1:max_iter | |||||
| % Check for convergence | |||||
| if norm(grad_f(xk)) < tol | |||||
| break; | |||||
| end | |||||
| dk = - grad_f(xk); % Steepset descent direction | |||||
| gk = gamma_f(f, grad_f, dk, xk); % Calculate gamma | |||||
| x_next = xk + gk * dk; % Update step | |||||
| f_next = f(x_next); | |||||
| xk = x_next; % Update point | |||||
| x_vals = [x_vals, x_next]; % Store values | |||||
| f_vals = [f_vals, f_next]; % Store function values | |||||
| end | |||||
| end | |||||
+ 50
- 0
Work 3/scripts/method_SteepDesc_Proj.m
View File
| @@ -0,0 +1,50 @@ | |||||
| function [x_vals, f_vals, k] = method_SteepDesc_Proj(f, grad_f, xk, sk, limmits, tol, max_iter, mode) | |||||
| % f: Objective function | |||||
| % grad_f: Gradient of the function | |||||
| % xk: Initial point [x0; y0] | |||||
| % sk: Step size (fixed positive scalar) | |||||
| % limits: Bounds of the feasible set for each dimension | |||||
| % tol: Tolerance for stopping criterion | |||||
| % max_iter: Maximum number of iterations | |||||
| % x_vals: Vector with the (x,y) values until minimum | |||||
| % f_vals: Vector with f(x,y) values until minimum | |||||
| % k: Number of iterations | |||||
| if strcmp(mode, 'armijo') == 1 | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_armijo(f, grad_f, dk, xk); | |||||
| elseif strcmp(mode, 'minimized') == 1 | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_minimized(f, grad_f, dk, xk); | |||||
| else % mode == 'fixed' | |||||
| gamma_f = @(f, grad_f, dk, xk) gamma_fixed(f, grad_f, dk, xk); | |||||
| end | |||||
| % Project the first point if needed | |||||
| xk = ProjectionPoint(xk, limmits); | |||||
| % Storage for iterations, begin with the first point | |||||
| x_vals = xk; | |||||
| f_vals = f(xk); | |||||
| for k = 1:max_iter | |||||
| % Check for convergence | |||||
| if norm(grad_f(xk)) < tol | |||||
| break; | |||||
| end | |||||
| dk = - grad_f(xk); % Steepset descent direction | |||||
| % First calculate xk-bar and project it if nessesary | |||||
| xkbar = xk + sk * dk; | |||||
| xkbar = ProjectionPoint(xkbar, limmits); | |||||
| dk = (xkbar - xk); % Steepest descent projection direction | |||||
| gk = gamma_f(f, grad_f, dk, xk); % Calculate gamma | |||||
| x_next = xk + gk * dk; % Update step | |||||
| f_next = f(x_next); | |||||
| xk = x_next; % Update point | |||||
| x_vals = [x_vals, x_next]; % Store values | |||||
| f_vals = [f_vals, f_next]; % Store function values | |||||
| end | |||||
| end | |||||
+ 42
- 0
Work 3/scripts/plot3dFun.m
View File
| @@ -0,0 +1,42 @@ | |||||
| function plot3dFun(fun, x_lim, y_lim, size, plot_title, filename) | |||||
| % 3D plots a function | |||||
| % fun: The function to plot | |||||
| % x_lim: The range for x axis. ex: [-2, 2] | |||||
| % y_lim: The range for y axis. ex: [0, 2] | |||||
| % size: The number of points for each axis | |||||
| % plot_title: The latex title for the plot | |||||
| % | |||||
| global image_width, | |||||
| global image_height; | |||||
| % Generate a grid for x and y | |||||
| x_space = linspace(x_lim(1), x_lim(2), size); | |||||
| y_space = linspace(y_lim(1), y_lim(2), size); | |||||
| [X, Y] = meshgrid(x_space, y_space); | |||||
| % Evaluate the function on the grid | |||||
| for i = 1:size | |||||
| for j = 1:size | |||||
| % Pass each [x1; x2] as input to fun | |||||
| Z(i, j) = fun([X(i, j); Y(i, j)]); | |||||
| end | |||||
| end | |||||
| % 3D plot | |||||
| figure('Name', 'f(x,y)', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||||
| surf(X, Y, Z); | |||||
| % Customize the plot | |||||
| xlabel('x1'); % Label for x-axis | |||||
| ylabel('x2'); % Label for y-axis | |||||
| zlabel('f(x, y)'); % Label for z-axis | |||||
| title(plot_title, 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||||
| colorbar; | |||||
| % save the figure | |||||
| if strcmp(filename, '') == 0 | |||||
| print(gcf, filename, '-dpng', '-r300'); | |||||
| end | |||||
| end | |||||
+ 41
- 0
Work 3/scripts/plotContour.m
View File
| @@ -0,0 +1,41 @@ | |||||
| function plotContour(fun, x_lim, y_lim, size, plot_title, filename) | |||||
| % plot the contour of a function | |||||
| % fun: The function to plot | |||||
| % x_lim: The range for x axis. ex: [-2, 2] | |||||
| % y_lim: The range for y axis. ex: [0, 2] | |||||
| % size: The number of points for each axis | |||||
| % plot_title: The latex title for the plot | |||||
| % | |||||
| global image_width, | |||||
| global image_height; | |||||
| % Generate a grid for x and y | |||||
| x_space = linspace(x_lim(1), x_lim(2), size); | |||||
| y_space = linspace(y_lim(1), y_lim(2), size); | |||||
| [X, Y] = meshgrid(x_space, y_space); | |||||
| % Evaluate the function on the grid | |||||
| for i = 1:size | |||||
| for j = 1:size | |||||
| % Pass each [x1; x2] as input to fun | |||||
| Z(i, j) = fun([X(i, j); Y(i, j)]); | |||||
| end | |||||
| end | |||||
| % Contour | |||||
| figure('Name', 'Contours of f(x1,x2)', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||||
| contour(X, Y, Z); | |||||
| % Customize the plot | |||||
| xlabel('x1'); % Label for x-axis | |||||
| ylabel('x2'); % Label for y-axis | |||||
| title(plot_title, 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||||
| colorbar; | |||||
| % save the figure | |||||
| if strcmp(filename, '') == 0 | |||||
| print(gcf, filename, '-dpng', '-r300'); | |||||
| end | |||||
| end | |||||
+ 54
- 0
Work 3/scripts/plotConvCompare.m
View File
| @@ -0,0 +1,54 @@ | |||||
| function plotConvCompare(points_1, title_1, points_2, title_2, points_3, title_3, Min_point, plot_title, filename) | |||||
| % 3D plots a function | |||||
| % points: The points to plot | |||||
| % contur_fun: The function for contour plot | |||||
| % x_lim: The range for x axis. ex: [-2, 2] | |||||
| % y_lim: The range for y axis. ex: [0, 2] | |||||
| % size: The number of points for each axis | |||||
| % plot_title: The latex title for the plot | |||||
| % filename: The filename to save the plot (if exists) | |||||
| % | |||||
| global image_width, | |||||
| global image_height; | |||||
| distances_1 = sqrt((points_1(1, :) - Min_point(1)).^2 + (points_1(2, :) - Min_point(2)).^2); | |||||
| distances_2 = sqrt((points_2(1, :) - Min_point(1)).^2 + (points_2(2, :) - Min_point(2)).^2); | |||||
| distances_3 = sqrt((points_3(1, :) - Min_point(1)).^2 + (points_3(2, :) - Min_point(2)).^2); | |||||
| % 2D plot | |||||
| figure('Name', 'Convergence compare', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||||
| title(plot_title, 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||||
| % One | |||||
| subplot(3, 1, 1); | |||||
| plot(distances_1, '-o'); | |||||
| % Customize the plot | |||||
| ylabel(title_1, 'Interpreter', 'none'); | |||||
| xlabel('Step'); | |||||
| grid on | |||||
| % One | |||||
| subplot(3, 1, 2); | |||||
| plot(distances_2, '-o'); | |||||
| % Customize the plot | |||||
| ylabel(title_2, 'Interpreter', 'none'); | |||||
| xlabel('Step'); | |||||
| grid on | |||||
| % One | |||||
| subplot(3, 1, 3); | |||||
| plot(distances_3, '-o'); | |||||
| % Customize the plot | |||||
| ylabel(title_3, 'Interpreter', 'none'); | |||||
| xlabel('Step'); | |||||
| grid on | |||||
| % save the figure | |||||
| if strcmp(filename, '') == 0 | |||||
| print(gcf, filename, '-dpng', '-r300'); | |||||
| end | |||||
| end | |||||
+ 28
- 0
Work 3/scripts/plotItersOverGamma.m
View File
| @@ -0,0 +1,28 @@ | |||||
| function plotItersOverGamma(gamma, iterations, plot_title, filename) | |||||
| % 3D plots a function | |||||
| % fun: The points to plot | |||||
| % contur_fun: The function for contour plot | |||||
| % x_lim: The range for x axis. ex: [-2, 2] | |||||
| % y_lim: The range for y axis. ex: [0, 2] | |||||
| % size: The number of points for each axis | |||||
| % plot_title: The latex title for the plot | |||||
| % filename: The filename to save the plot (if exists) | |||||
| % | |||||
| global image_width, | |||||
| global image_height; | |||||
| figure('Name', 'Iterations_over_gamma', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||||
| plot(gamma, iterations, '*r', 'LineWidth', 2); | |||||
| % Customize the plot | |||||
| title(plot_title, 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||||
| xlabel('\gamma') ; | |||||
| ylabel('Iterations'); | |||||
| % save the figure | |||||
| if strcmp(filename, '') == 0 | |||||
| print(gcf, filename, '-dpng', '-r300'); | |||||
| end | |||||
| end | |||||
+ 48
- 0
Work 3/scripts/plotPointsOverContour.m
View File
| @@ -0,0 +1,48 @@ | |||||
| function plotPointsOverContour(points, contour_fun, x_lim, y_lim, size, plot_title, filename) | |||||
| % 3D plots a function | |||||
| % points: The points to plot | |||||
| % contur_fun: The function for contour plot | |||||
| % x_lim: The range for x axis. ex: [-2, 2] | |||||
| % y_lim: The range for y axis. ex: [0, 2] | |||||
| % size: The number of points for each axis | |||||
| % plot_title: The latex title for the plot | |||||
| % filename: The filename to save the plot (if exists) | |||||
| % | |||||
| global image_width, | |||||
| global image_height; | |||||
| % Generate a grid for x and y | |||||
| x_space = linspace(x_lim(1), x_lim(2), size); | |||||
| y_space = linspace(y_lim(1), y_lim(2), size); | |||||
| [X, Y] = meshgrid(x_space, y_space); | |||||
| % Evaluate the function on the grid | |||||
| for i = 1:size | |||||
| for j = 1:size | |||||
| % Pass each [x1; x2] as input to fun | |||||
| Z(i, j) = contour_fun([X(i, j); Y(i, j)]); | |||||
| end | |||||
| end | |||||
| % 2D plot | |||||
| figure('Name', '(x1,x2) convergence', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||||
| plot(points(1, :), points(2, :), '-or'); | |||||
| hold on | |||||
| contour(X, Y, Z); | |||||
| % Customize the plot | |||||
| xlim(x_lim); | |||||
| ylim(y_lim); | |||||
| xlabel('x1'); % Label for x-axis | |||||
| ylabel('x2'); % Label for y-axis | |||||
| grid on | |||||
| title(plot_title, 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||||
| colorbar; | |||||
| % save the figure | |||||
| if strcmp(filename, '') == 0 | |||||
| print(gcf, filename, '-dpng', '-r300'); | |||||
| end | |||||
| end | |||||