31 changed files with 441 additions and 303 deletions
Unified View
Diff Options
-
+17 -16Work 1/scripts/GivenEnv.m
-
+37 -0Work 1/scripts/Work1.m
-
+0 -48Work 1/scripts/bisection/bisection_interval.m
-
+0 -41Work 1/scripts/bisection/bisection_over_epsilon.m
-
+0 -44Work 1/scripts/bisection/bisection_over_lambda.m
-
+62 -0Work 1/scripts/bisection_over_epsilon.m
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_der_fun1.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_der_fun2.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_der_fun3.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_fun1.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_fun2.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_bisection_fun3.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_fibonacci_fun1.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_fibonacci_fun2.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_fibonacci_fun3.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_golden_section_fun1.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_golden_section_fun2.png
-
BINWork 1/scripts/figures/interval_over_iterations_min_golden_section_fun3.png
-
BINWork 1/scripts/figures/iter_over_epsilon_min_bisection.png
-
BINWork 1/scripts/figures/iter_over_lambda_min_bisection.png
-
BINWork 1/scripts/figures/iter_over_lambda_min_bisection_der.png
-
BINWork 1/scripts/figures/iter_over_lambda_min_fibonacci.png
-
BINWork 1/scripts/figures/iter_over_lambda_min_golden_section.png
-
+0 -45Work 1/scripts/golden_section/golden_section_interval.m
-
+0 -39Work 1/scripts/golden_section/golden_section_over_lambda.m
-
+82 -0Work 1/scripts/interval_over_iterations.m
-
+83 -0Work 1/scripts/iterations_over_lambda.m
-
+34 -33Work 1/scripts/min_bisection.m
-
+36 -0Work 1/scripts/min_bisection_der.m
-
+54 -0Work 1/scripts/min_fibonacci.m
-
+36 -37Work 1/scripts/min_golden_section.m
+ 17
- 16
Work 1/scripts/GivenEnv.m
View File
| @@ -1,16 +1,17 @@ | |||||
| % | |||||
| % Select the given interval: [-1,3] | |||||
| a_0 = -1; | |||||
| b_0 = 3; | |||||
| % Setup the functions under test | |||||
| f_1 = @(x) (x-2)^2 + x*log(x+3); | |||||
| f_2 = @(x) exp(-2*x) + (x-2)^2; | |||||
| f_3 = @(x) exp(x)*(x^3 - 1) + (x-1)*sin(x); | |||||
| funs = {f_1, f_2, f_3}; | |||||
| % Setup the function titles | |||||
| title_f1 = "$f_1(x) = (x - 2)^2 + x \cdot \ln(x + 3)$"; | |||||
| title_f2 = "$f_2(x) = e^{-2x} + (x - 2)^2$"; | |||||
| title_f3 = "$f_3(x) = e^x \cdot (x^3 - 1) + (x - 1) \cdot \sin(x)$"; | |||||
| titles = [title_f1; title_f2; title_f3]; | |||||
| % | |||||
| % Select the given interval: [-1,3] | |||||
| a_0 = -1; | |||||
| b_0 = 3; | |||||
| % Setup the functions under test | |||||
| syms x; | |||||
| f_1 = (x-2)^2 + x*log(x+3); | |||||
| f_2 = exp(-2*x) + (x-2)^2; | |||||
| f_3 = exp(x)*(x^3 - 1) + (x-1)*sin(x); | |||||
| funs = [f_1; f_2; f_3]; | |||||
| % Setup the function titles | |||||
| title_f1 = "$f_1(x) = (x - 2)^2 + x \cdot \ln(x + 3)$"; | |||||
| title_f2 = "$f_2(x) = e^{-2x} + (x - 2)^2$"; | |||||
| title_f3 = "$f_3(x) = e^x \cdot (x^3 - 1) + (x - 1) \cdot \sin(x)$"; | |||||
| titles = [title_f1; title_f2; title_f3]; | |||||
+ 37
- 0
Work 1/scripts/Work1.m
View File
| @@ -0,0 +1,37 @@ | |||||
| % | |||||
| % | |||||
| % | |||||
| % | |||||
| % | |||||
| % | |||||
| disp (" "); | |||||
| disp (" "); | |||||
| disp ('1. Number of iterations for different epsilon values for min_bisection'); | |||||
| disp ('----'); | |||||
| bisection_over_epsilon; | |||||
| methods = { | |||||
| @min_bisection; | |||||
| @min_golden_section; | |||||
| @min_fibonacci; | |||||
| @min_bisection_der | |||||
| }; | |||||
| disp (" "); | |||||
| disp (" "); | |||||
| disp ('2. Number of iterations for different lambda values'); | |||||
| disp ('----'); | |||||
| for i = 1:length(methods) | |||||
| iterations_over_lambda(methods{i}); | |||||
| end | |||||
| disp (" "); | |||||
| disp (" "); | |||||
| disp ('3. [a, b] interval convergence'); | |||||
| disp ('----'); | |||||
| for i = 1:length(methods) | |||||
| interval_over_iterations(methods{i}); | |||||
| end | |||||
+ 0
- 48
Work 1/scripts/bisection/bisection_interval.m
View File
| @@ -1,48 +0,0 @@ | |||||
| % | |||||
| % Keeping epsilon fixed, plot the [a,b] interval over the iterations for | |||||
| % different lambda values (min, mid, max)) | |||||
| % | |||||
| % Clear workspace and load the functions and interval | |||||
| clear | |||||
| addpath('..'); | |||||
| GivenEnv; | |||||
| % * epsilon: e = 0.001 | |||||
| % * lambda: l > 2e = 0.001 | |||||
| % * dl: A small step away from 2e | |||||
| % dl = 0.0001 | |||||
| % * lambda_max: 0.1 | |||||
| % * N: 3 lambda values | |||||
| N = 3; | |||||
| epsilon = 0.001; | |||||
| dl = 0.0001; | |||||
| lambda_max= 0.1; | |||||
| lambda = linspace(2*epsilon + dl, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % * Call the bisection method for each lambda value for each function | |||||
| % * Plot the [a,b] interval over iterations for each lambda for each function | |||||
| % | |||||
| for i = 1:length(funs) | |||||
| figure; | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = bisection(funs{i}, a_0, b_0, epsilon, lambda(j)); | |||||
| subplot(length(funs), 1, j) | |||||
| plot(1:length(a), a, 'ob') | |||||
| hold on | |||||
| plot(1:length(b), b, '*r') | |||||
| if j == 1 | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| end | |||||
| xlabel("Iterations @lambda=" + lambda(j)) | |||||
| ylabel('[a_k, b_k]') | |||||
| end | |||||
| end | |||||
+ 0
- 41
Work 1/scripts/bisection/bisection_over_epsilon.m
View File
| @@ -1,41 +0,0 @@ | |||||
| % | |||||
| % Keeping lambda (accuracy) fixed, test the iteration needed for different | |||||
| % epsilon values. | |||||
| % | |||||
| % Clear workspace and load the functions and interval | |||||
| clear | |||||
| addpath('..'); | |||||
| GivenEnv; | |||||
| % * lambda = 0.01 | |||||
| % * epsilon: e < lambda/2 = 0.005 | |||||
| % * de: A small step away from zero and lambda/2 | |||||
| % de = 0.0001 | |||||
| % * N: 50 points | |||||
| N = 50; | |||||
| lambda = 0.01; | |||||
| de = 0.0001; | |||||
| epsilon = linspace(de, (lambda/2)-de, N); | |||||
| k = zeros(1,N); % preallocate k | |||||
| % | |||||
| % * Call the bisection method for each epsilon value for each function and | |||||
| % keep the number of iterations needed. | |||||
| % * Plot the iterations k(epsilon) for each function | |||||
| % | |||||
| for i = 1:length(funs) | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = bisection(funs{i}, a_0, b_0, epsilon(j), lambda); | |||||
| end | |||||
| subplot(1, length(funs), i) | |||||
| plot(epsilon, k, '-b', 'LineWidth', 1.0) | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| xlabel('epsilon') | |||||
| ylabel('Iterations') | |||||
| end | |||||
+ 0
- 44
Work 1/scripts/bisection/bisection_over_lambda.m
View File
| @@ -1,44 +0,0 @@ | |||||
| % | |||||
| % Keeping epsilon fixed, test the iteration needed for different lambda | |||||
| % values. | |||||
| % | |||||
| % Clear workspace and load the functions and interval | |||||
| clear | |||||
| addpath('..'); | |||||
| GivenEnv; | |||||
| % * epsilon: e = 0.001 | |||||
| % * lambda: l > 2e = 0.001 | |||||
| % * dl: A small step away from 2e | |||||
| % dl = 0.0001 | |||||
| % * lambda_max: 0.1 | |||||
| % * N: 50 points | |||||
| N = 50; | |||||
| epsilon = 0.001; | |||||
| dl = 0.0001; | |||||
| lambda_max= 0.1; | |||||
| lambda = linspace(2*epsilon + dl, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % * Call the bisection method for each lambda value for each function and | |||||
| % keep the number of iterations needed. | |||||
| % * Plot the iterations k(lambda) for each function | |||||
| % | |||||
| for i = 1:length(funs) | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = bisection(funs{i}, a_0, b_0, epsilon, lambda(j)); | |||||
| end | |||||
| subplot(1, length(funs), i) | |||||
| plot(lambda, k, '-b', 'LineWidth', 1.0) | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| xlabel('lambda') | |||||
| ylabel('Iterations') | |||||
| end | |||||
+ 62
- 0
Work 1/scripts/bisection_over_epsilon.m
View File
| @@ -0,0 +1,62 @@ | |||||
| % | |||||
| % Keeping lambda (accuracy) fixed, test the iteration needed for different | |||||
| % epsilon values. | |||||
| % | |||||
| % Load the functions and interval | |||||
| GivenEnv; | |||||
| fig_dir = 'figures'; | |||||
| if ~exist(fig_dir, 'dir') | |||||
| mkdir(fig_dir); | |||||
| end | |||||
| % Setup | |||||
| % ======================== | |||||
| % lambda = 0.01 | |||||
| % epsilon: e < lambda/2 = 0.005 | |||||
| % de: A small step away from zero and lambda/2 | |||||
| % de = 0.0001 | |||||
| % N: 50 points (50 epsilon values) | |||||
| N = 50; | |||||
| lambda = 0.01; | |||||
| de = 0.0001; | |||||
| epsilon = linspace(de, (lambda/2)-de, N); | |||||
| k = zeros(1,N); % preallocate k | |||||
| % | |||||
| % Call the min_bisection method for each epsilon value for each | |||||
| % function and keep the number of iterations needed. | |||||
| % Then plot and save the # of iterations k(epsilon) for each function. | |||||
| % | |||||
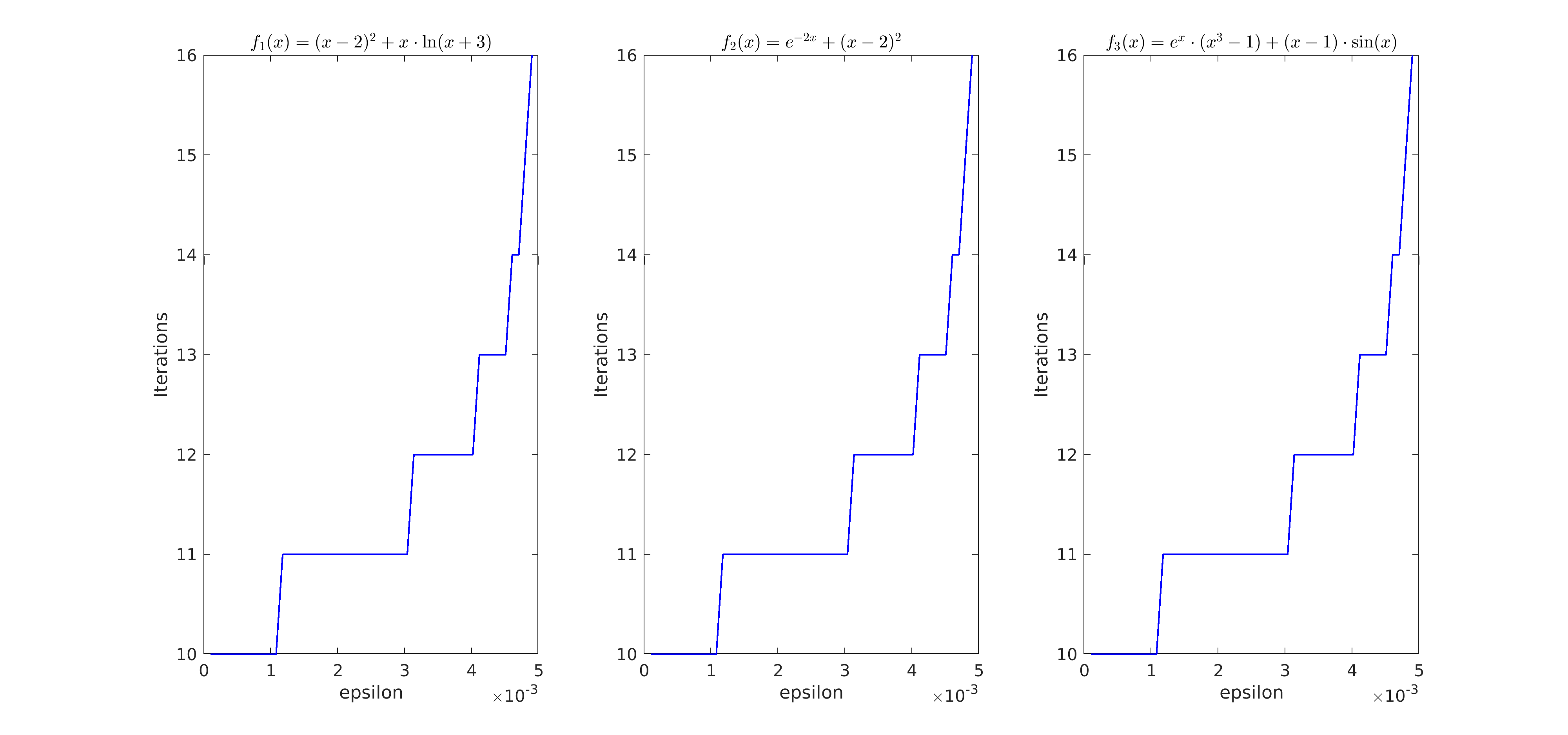
| figure('Name', 'iterations_over_epsilon_min_bisection', 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, 1280, 600]); % Set the figure size to HD | |||||
| for i = 1:length(funs) | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = min_bisection(funs(i), a_0, b_0, epsilon(j), lambda); | |||||
| end | |||||
| fprintf('%20s(%34s ): [a, b]= [%f, %f], iterations(min, max)= (%d, %d)\n', ... | |||||
| "min_bisection", char(funs(i)), a(end), b(end), k(1), k(N) ); | |||||
| subplot(1, length(funs), i) | |||||
| plot(epsilon, k, '-b', 'LineWidth', 1.0) | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| xlabel('epsilon') | |||||
| ylabel('Iterations') | |||||
| end | |||||
| % | |||||
| % Print and save the figures | |||||
| % | |||||
| %fig_epsc = fullfile(fig_dir, "iter_over_epsilon_min_bisection" + ".epsc"); | |||||
| fig_png = fullfile(fig_dir, "iter_over_epsilon_min_bisection" + ".png"); | |||||
| %print(gcf, fig_epsc, '-depsc', '-r300'); | |||||
| print(gcf, fig_png, '-dpng', '-r300'); | |||||
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_der_fun1.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_der_fun2.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_der_fun3.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_fun1.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_fun2.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_bisection_fun3.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_fibonacci_fun1.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_fibonacci_fun2.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_fibonacci_fun3.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_golden_section_fun1.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_golden_section_fun2.png
View File
BIN
Work 1/scripts/figures/interval_over_iterations_min_golden_section_fun3.png
View File
BIN
Work 1/scripts/figures/iter_over_epsilon_min_bisection.png
View File
BIN
Work 1/scripts/figures/iter_over_lambda_min_bisection.png
View File
BIN
Work 1/scripts/figures/iter_over_lambda_min_bisection_der.png
View File
BIN
Work 1/scripts/figures/iter_over_lambda_min_fibonacci.png
View File
BIN
Work 1/scripts/figures/iter_over_lambda_min_golden_section.png
View File
+ 0
- 45
Work 1/scripts/golden_section/golden_section_interval.m
View File
| @@ -1,45 +0,0 @@ | |||||
| % | |||||
| % Plot the [a,b] interval over the iterations for different lambda | |||||
| % values (min, mid, max)) | |||||
| % | |||||
| % Clear workspace and load the functions and interval | |||||
| clear | |||||
| addpath('..'); | |||||
| GivenEnv; | |||||
| % * lambda_min: 0.0001 | |||||
| % * lambda_max: 0.1 | |||||
| % * N: 3 lambda values | |||||
| N = 3; | |||||
| lambda_min = 0.0001; | |||||
| lambda_max = 0.1; | |||||
| lambda = linspace(lambda_min, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % * Call the golden_sector method for each lambda value for each function and | |||||
| % keep the number of iterations needed. | |||||
| % * Plot the [a,b] interval over iterations for each lambda for each function | |||||
| % | |||||
| for i = 1:length(funs) | |||||
| figure; | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = golden_section(funs{i}, a_0, b_0, lambda(j)); | |||||
| subplot(length(funs), 1, j) | |||||
| plot(1:length(a), a, 'ob') | |||||
| hold on | |||||
| plot(1:length(b), b, '*r') | |||||
| if j == 1 | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| end | |||||
| xlabel("Iterations @lambda=" + lambda(j)) | |||||
| ylabel('[a_k, b_k]') | |||||
| end | |||||
| end | |||||
+ 0
- 39
Work 1/scripts/golden_section/golden_section_over_lambda.m
View File
| @@ -1,39 +0,0 @@ | |||||
| % | |||||
| % Test the iteration needed for different lambda values. | |||||
| % | |||||
| % Clear workspace and load the functions and interval | |||||
| clear | |||||
| addpath('..'); | |||||
| GivenEnv; | |||||
| % * lambda_min: 0.0001 | |||||
| % * lambda_max: 0.1 | |||||
| % * N: 50 points | |||||
| N = 50; | |||||
| lambda_min = 0.0001; | |||||
| lambda_max = 0.1; | |||||
| lambda = linspace(lambda_min, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % * Call the golden_sector method for each lambda value for each function and | |||||
| % keep the number of iterations needed. | |||||
| % * Plot the iterations k(lambda) for each function | |||||
| % | |||||
| for i = 1:length(funs) | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = golden_section(funs{i}, a_0, b_0, lambda(j)); | |||||
| end | |||||
| subplot(1, length(funs), i) | |||||
| plot(lambda, k, '-b', 'LineWidth', 1.0) | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| xlabel('lambda') | |||||
| ylabel('Iterations') | |||||
| end | |||||
+ 82
- 0
Work 1/scripts/interval_over_iterations.m
View File
| @@ -0,0 +1,82 @@ | |||||
| function [] = interval_over_iterations(method) | |||||
| % Plot the [a,b] interval over the iterations for different lambda | |||||
| % values (min, mid, max)) | |||||
| % | |||||
| % method: the minimum calculation method | |||||
| % * bisections | |||||
| % * golden_section | |||||
| % * fibonacci | |||||
| % * bisection_der | |||||
| % Load the functions and interval | |||||
| GivenEnv; | |||||
| fig_dir = 'figures'; | |||||
| if ~exist(fig_dir, 'dir') | |||||
| mkdir(fig_dir); | |||||
| end | |||||
| % Setup | |||||
| % ======================== | |||||
| % | |||||
| % We need to test against the same lambda values for all the methods in | |||||
| % order to compare them. And since epsilon (which is related to lambda) | |||||
| % was given for bisection method, we base our calculations to that. | |||||
| % | |||||
| % | |||||
| % epsilon: e = 0.001 | |||||
| % lambda: l > 2e => | |||||
| % lambda_min: 0.0021 | |||||
| % lambda_max: 0.1 | |||||
| % N: 3 points (3 lambda values min-mid-max) | |||||
| N = 3; | |||||
| epsilon = 0.001; | |||||
| lambda_min = 0.0021; | |||||
| lambda_max = 0.1; | |||||
| lambda = linspace(lambda_min, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % Call the minimum calculation method for each lambda value for each | |||||
| % function and keep the number of iterations needed. | |||||
| % Then Plot the [a,b] interval over iterations for each lambda for each | |||||
| % function. | |||||
| % | |||||
| % note: In order to use the same method call for all methods, we force a | |||||
| % common interface for minimum method functions. Thus some arguments | |||||
| % will not be needed for some methods (epsilon is not needed for | |||||
| % bisection _der for example). | |||||
| % | |||||
| disp(" "); | |||||
| for i = 1:length(funs) | |||||
| figure('Name', "interval_over_iterations_" + char(method) + "_fun" + i, 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, 1280, 720]); % Set the figure size to HD | |||||
| for j = 1:N | |||||
| [a, b, k(j)] = method(funs(i), a_0, b_0, epsilon, lambda(j)); | |||||
| fprintf('%20s(%34s ): [a, b]= [%f, %f], @lambda=%f, iterations= %d\n', ... | |||||
| char(method), char(funs(i)), a(end), b(end), lambda(j), k(j) ); | |||||
| subplot(length(funs), 1, j) | |||||
| plot(1:length(a), a, 'ob') | |||||
| hold on | |||||
| plot(1:length(b), b, '*r') | |||||
| if j == 1 | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| end | |||||
| xlabel("Iterations @lambda=" + lambda(j)) | |||||
| ylabel('[a_k, b_k]') | |||||
| end | |||||
| % Print and save the figure | |||||
| %fig_epsc = fullfile(fig_dir, "interval_over_iterations_" + char(method) + "_fun" + i + ".epsc"); | |||||
| fig_png = fullfile(fig_dir, "interval_over_iterations_" + char(method) + "_fun" + i + ".png"); | |||||
| %print(gcf, fig_epsc, '-depsc', '-r300'); | |||||
| print(gcf, fig_png, '-dpng', '-r300'); | |||||
| end | |||||
+ 83
- 0
Work 1/scripts/iterations_over_lambda.m
View File
| @@ -0,0 +1,83 @@ | |||||
| function [] = iterations_over_lambda(method) | |||||
| % Plot iteration needed for different lambda values. | |||||
| % | |||||
| % | |||||
| % method: the minimum calculation method | |||||
| % * bisections | |||||
| % * golden_section | |||||
| % * fibonacci | |||||
| % * bisection_der | |||||
| % Load the functions and interval | |||||
| GivenEnv; | |||||
| fig_dir = 'figures'; | |||||
| if ~exist(fig_dir, 'dir') | |||||
| mkdir(fig_dir); | |||||
| end | |||||
| % Setup | |||||
| % ======================== | |||||
| % | |||||
| % We need to test against the same lambda values for all the methods in | |||||
| % order to compare them. And since epsilon (which is related to lambda) | |||||
| % was given for bisection method, we base our calculations to that. | |||||
| % | |||||
| % | |||||
| % epsilon: e = 0.001 | |||||
| % lambda: l > 2e => | |||||
| % lambda_min: 0.0021 | |||||
| % lambda_max: 0.1 | |||||
| % N: 50 points (50 lambda values) | |||||
| N = 50; | |||||
| epsilon = 0.001; | |||||
| lambda_min = 0.0021; | |||||
| lambda_max = 0.1; | |||||
| lambda = linspace(lambda_min, lambda_max, N); | |||||
| k = zeros(1, N); % preallocate k | |||||
| % | |||||
| % Call the minimum calculation method for each lambda value for each | |||||
| % function and keep the number of iterations needed. | |||||
| % Then plot and save the # of iterations k(lambda) for each function. | |||||
| % | |||||
| % note: In order to use the same method call for all methods, we force a | |||||
| % common interface for minimum method functions. Thus some arguments | |||||
| % will not be needed for some methods (epsilon is not needed for | |||||
| % bisection _der for example). | |||||
| % | |||||
| figure('Name', "iterations_over_lambda_" + char(method), 'NumberTitle', 'off'); | |||||
| set(gcf, 'Position', [100, 100, 1280, 600]); % Set the figure size to HD | |||||
| disp(" "); | |||||
| for i = 1:length(funs) | |||||
| for j = N:-1:1 | |||||
| [a, b, k(j)] = method(funs(i), a_0, b_0, epsilon, lambda(j)); | |||||
| end | |||||
| fprintf('%20s(%34s ): [a, b]= [%f, %f], iterations(min, max)= (%d, %d)\n', ... | |||||
| char(method), char(funs(i)), a(end), b(end), k(N), k(1) ); | |||||
| subplot(1, length(funs), i) | |||||
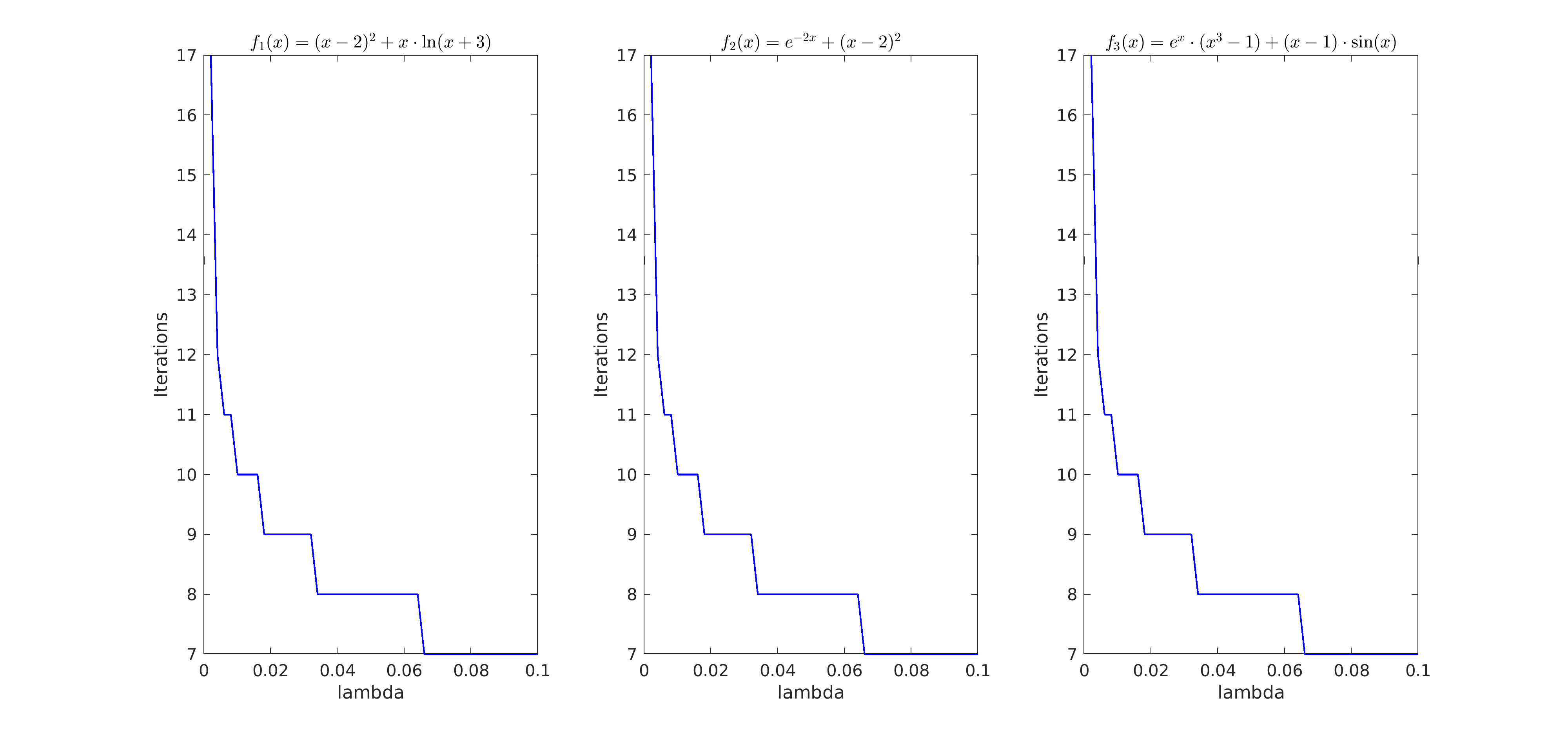
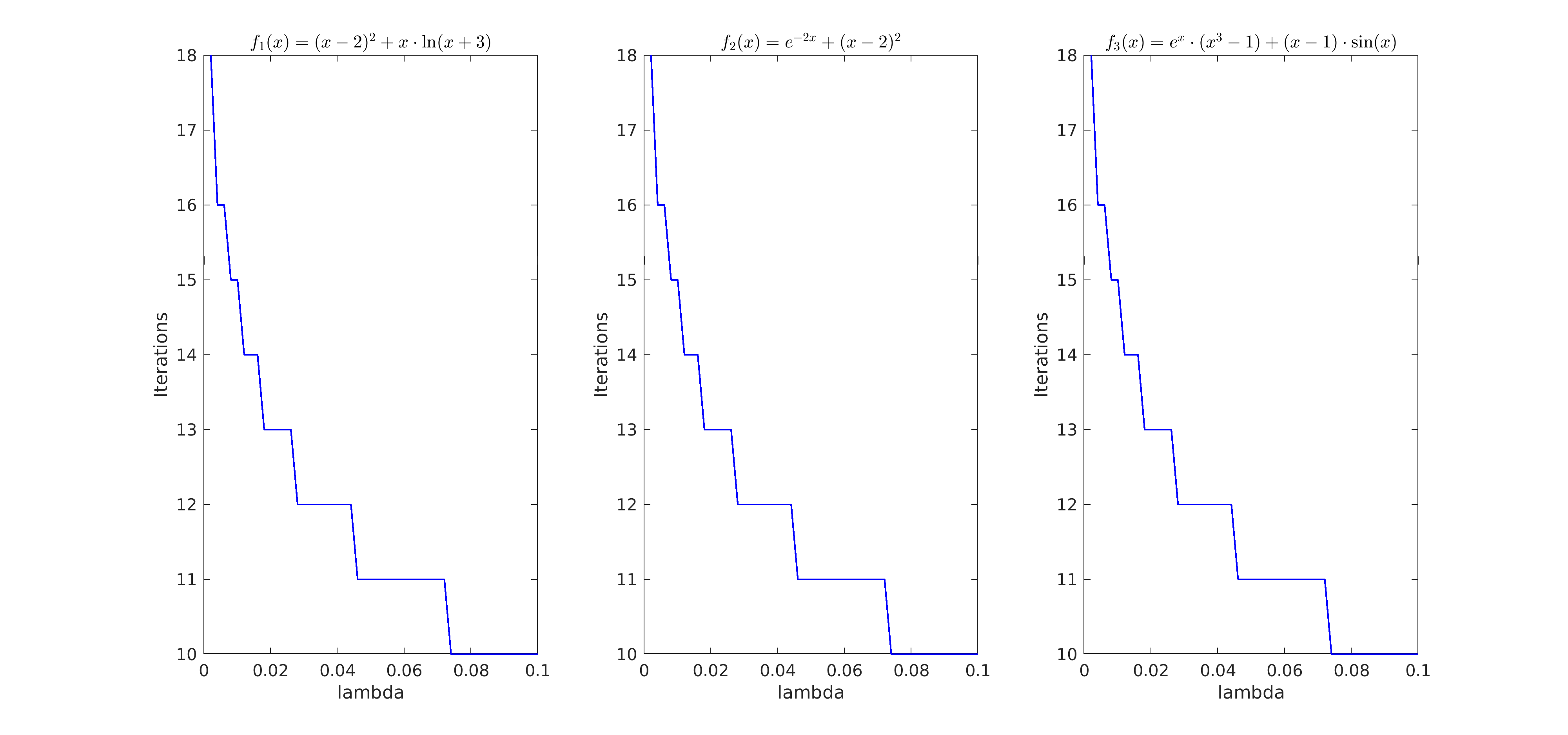
| plot(lambda, k, '-b', 'LineWidth', 1.0) | |||||
| title(titles(i), 'Interpreter', 'latex') | |||||
| xlabel('lambda') | |||||
| ylabel('Iterations') | |||||
| end | |||||
| % | |||||
| % Print and save the figures | |||||
| % | |||||
| %fig_epsc = fullfile(fig_dir, "iter_over_lambda_" + char(method) + ".epsc"); | |||||
| fig_png = fullfile(fig_dir, "iter_over_lambda_" + char(method) + ".png"); | |||||
| %print(gcf, fig_epsc, '-depsc', '-r300'); | |||||
| print(gcf, fig_png, '-dpng', '-r300'); | |||||
Work 1/scripts/bisection/bisection.m → Work 1/scripts/min_bisection.m
View File
| @@ -1,33 +1,34 @@ | |||||
| function [a, b, k] = bisection(fun, alpha, beta, epsilon, lambda) | |||||
| % | |||||
| % Detailed explanation goes here | |||||
| % | |||||
| % | |||||
| % Error checking | |||||
| if 2*epsilon >= lambda || lambda <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init output vectors | |||||
| a = alpha; | |||||
| b = beta; | |||||
| k=1; | |||||
| while b(k) - a(k) > lambda | |||||
| % bisect [a,b] | |||||
| mid = (a(k) + b(k)) / 2; | |||||
| x_1 = mid - epsilon; | |||||
| x_2 = mid + epsilon; | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_2; | |||||
| else | |||||
| a(k) = x_1; | |||||
| b(k) = b(k-1); | |||||
| end | |||||
| end | |||||
| function [a, b, k] = min_bisection(fun_expression, alpha, beta, epsilon, lambda) | |||||
| % | |||||
| % Detailed explanation goes here | |||||
| % | |||||
| % | |||||
| % Error checking | |||||
| if 2*epsilon >= lambda || lambda <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init | |||||
| a = alpha; | |||||
| b = beta; | |||||
| fun = matlabFunction(fun_expression); | |||||
| k=1; | |||||
| while b(k) - a(k) > lambda | |||||
| % bisect [a,b] | |||||
| mid = (a(k) + b(k)) / 2; | |||||
| x_1 = mid - epsilon; | |||||
| x_2 = mid + epsilon; | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_2; | |||||
| else | |||||
| a(k) = x_1; | |||||
| b(k) = b(k-1); | |||||
| end | |||||
| end | |||||
+ 36
- 0
Work 1/scripts/min_bisection_der.m
View File
| @@ -0,0 +1,36 @@ | |||||
| function [a, b, k] = min_bisection_der(fun_expression, alpha, beta, epsilon, lambda) | |||||
| % | |||||
| % Detailed explanation goes here | |||||
| % | |||||
| % | |||||
| % Error checking | |||||
| if lambda <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init output vectors | |||||
| a = alpha; | |||||
| b = beta; | |||||
| dfun = matlabFunction(diff(fun_expression)); | |||||
| k=1; | |||||
| while b(k) - a(k) > lambda | |||||
| % bisect [a,b] | |||||
| x_mid = (a(k) + b(k)) / 2; | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| df = dfun(x_mid); | |||||
| if df < 0 | |||||
| a(k) = x_mid; | |||||
| b(k) = b(k-1); | |||||
| elseif df > 0 | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_mid; | |||||
| else % df == 0 | |||||
| a(k) = x_mid; | |||||
| b(k) = x_mid; | |||||
| break; | |||||
| end | |||||
| end | |||||
+ 54
- 0
Work 1/scripts/min_fibonacci.m
View File
| @@ -0,0 +1,54 @@ | |||||
| function [a, b, N] = min_fibonacci(fun_expression, alpha, beta, epsilon, lambda) | |||||
| % | |||||
| % Use Binet's formula instead of matlab's recursive fibonacci | |||||
| % implementation | |||||
| fib = @(n) ( ((1 + sqrt(5))^n - (1 - sqrt(5))^n) / (2^n * sqrt(5)) ); | |||||
| % Error checking | |||||
| if lambda <= 0 || epsilon <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init variables | |||||
| a = alpha; | |||||
| b = beta; | |||||
| fun = matlabFunction(fun_expression); | |||||
| % calculate number of iterations | |||||
| N=0; | |||||
| while fibonacci(N) < (b(1) - a(1)) / lambda | |||||
| N = N + 1; | |||||
| end | |||||
| % calculate x1, x2 of the first iteration, since the following iteration | |||||
| % will not require to calculate both | |||||
| x_1 = a(1) + (fib(N-2) / fib(N)) * (b(1) - a(1)); | |||||
| x_2 = a(1) + (fib(N-1) / fib(N)) * (b(1) - a(1)); | |||||
| % All but the last calculation | |||||
| for k = 1:N-2 | |||||
| % set new search interval | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k+1) = a(k); | |||||
| b(k+1) = x_2; | |||||
| x_2 = x_1; | |||||
| x_1 = a(k+1) + (fib(N-k-2) / fib(N-k)) * (b(k+1) - a(k+1)); | |||||
| else | |||||
| a(k+1) = x_1; | |||||
| b(k+1) = b(k); | |||||
| x_1 = x_2; | |||||
| x_2 = a(k+1) + (fib(N-k-1) / fib(N-k)) * (b(k+1) - a(k+1)); | |||||
| end | |||||
| end | |||||
| % Last calculation | |||||
| x_2 = x_1 + epsilon; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(N) = a(N-1); | |||||
| b(N) = x_1; | |||||
| else | |||||
| a(N) = x_1; | |||||
| b(N) = b(N-1); | |||||
| end | |||||
Work 1/scripts/golden_section/golden_section.m → Work 1/scripts/min_golden_section.m
View File
| @@ -1,37 +1,36 @@ | |||||
| function [a, b, k] = golden_section(fun, alpha, beta, lambda) | |||||
| % | |||||
| % Error checking | |||||
| if lambda <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init variables | |||||
| gamma = 0.618; | |||||
| a = alpha; | |||||
| b = beta; | |||||
| % calculate x1, x2 of the first iteration, since the following iteration | |||||
| % will not require to calculate both | |||||
| k=1; | |||||
| x_1 = a(k) + (1 - gamma)*(b(k) - a(k)); | |||||
| x_2 = a(k) + gamma*(b(k) - a(k)); | |||||
| while b(k) - a(k) > lambda | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_2; | |||||
| x_2 = x_1; | |||||
| x_1 = a(k) + (1 - gamma)*(b(k) - a(k)); | |||||
| else | |||||
| a(k) = x_1; | |||||
| b(k) = b(k-1); | |||||
| x_1 = x_2; | |||||
| x_2 = a(k) + gamma*(b(k) - a(k)); | |||||
| end | |||||
| end | |||||
| function [a, b, k] = min_golden_section(fun_expression, alpha, beta, epsilon, lambda) | |||||
| % | |||||
| % Error checking | |||||
| if lambda <= 0 | |||||
| error ('Convergence criteria not met') | |||||
| end | |||||
| % Init variables | |||||
| gamma = 0.618; | |||||
| a = alpha; | |||||
| b = beta; | |||||
| fun = matlabFunction(fun_expression); | |||||
| % calculate x1, x2 of the first iteration, since the following iteration | |||||
| % will not require to calculate both | |||||
| k=1; | |||||
| x_1 = a(k) + (1 - gamma)*(b(k) - a(k)); | |||||
| x_2 = a(k) + gamma*(b(k) - a(k)); | |||||
| while b(k) - a(k) > lambda | |||||
| % set new search interval | |||||
| k = k + 1; | |||||
| if fun(x_1) < fun(x_2) | |||||
| a(k) = a(k-1); | |||||
| b(k) = x_2; | |||||
| x_2 = x_1; | |||||
| x_1 = a(k) + (1 - gamma)*(b(k) - a(k)); | |||||
| else | |||||
| a(k) = x_1; | |||||
| b(k) = b(k-1); | |||||
| x_1 = x_2; | |||||
| x_2 = a(k) + gamma*(b(k) - a(k)); | |||||
| end | |||||
| end | |||||