25 değiştirilmiş dosya ile 414 ekleme ve 163 silme
Görünümü Böl
Diff Seçenekleri
-
BINWork2/report/Work2_report.pdf
-
+79 -10Work2/report/Work2_report.tex
-
+2 -1Work2/scripts/GivenEnv.m
-
+67 -15Work2/scripts/Script_2_Steepest_descent.m
-
+36 -44Work2/scripts/Script_3_Newton.m
-
+97 -34Work2/scripts/Script_4_LevMar.m
-
BINWork2/scripts/figures/LevMar_fixed_2.png
-
BINWork2/scripts/figures/LevMar_fixed_3.png
-
BINWork2/scripts/figures/LevMar_minimized_2.png
-
BINWork2/scripts/figures/LevMar_minimized_3.png
-
BINWork2/scripts/figures/StDes_Iter_o_gamma_2.png
-
BINWork2/scripts/figures/StDes_armijo_2.png
-
BINWork2/scripts/figures/StDes_armijo_3.png
-
BINWork2/scripts/figures/StDes_fixed_2.png
-
BINWork2/scripts/figures/StDes_fixed_3.png
-
BINWork2/scripts/figures/StDes_minimized_2.png
-
BINWork2/scripts/figures/StDes_minimized_3.png
-
+49 -0Work2/scripts/fmin_bisection.m
-
+17 -9Work2/scripts/gamma_armijo.m
-
+1 -1Work2/scripts/gamma_fixed.m
-
+19 -13Work2/scripts/gamma_minimized.m
-
+24 -13Work2/scripts/method_lev_mar.m
-
+11 -11Work2/scripts/method_newton.m
-
+11 -11Work2/scripts/method_steepest_descent.m
-
+1 -1Work2/scripts/plotPointsOverContour.m
BIN
Work2/report/Work2_report.pdf
Dosyayı Görüntüle
+ 79
- 10
Work2/report/Work2_report.tex
Dosyayı Görüntüle
| @@ -74,7 +74,7 @@ | |||
| \subsection{Κλήση μεθόδων επιλογής βήματος $\gamma_k$} | |||
| \label{subsec:polymorphic-calls} | |||
| Δεδομένου ότι οι μέθοδοι θα πρέπει να καλεστούν και εκτελεστούν με παραπάνω από μία τεχνική επιλογής βήματος $\gamma_k$, δημιουργήσαμε εσωτερικά της κάθε μεθόδου ένα κοινό interface για τις μεθόδους επιλογής βήματος. | |||
| Αυτό έχει τη μορφή: \textit{\textbf{gamma\_<method>(f, grad\_f, x0)}}, όπου το \textbf{f} είναι η αντικειμενική συνάρτηση, \textbf{grad\_f} η συνάρτηση κλίσης και \textbf{x0} το σημείο ενδιαφέροντος. | |||
| Αυτό έχει τη μορφή: \textit{\textbf{gamma\_<method>(f, dk, xk)}}, όπου το \textbf{f} είναι η αντικειμενική συνάρτηση, \textbf{dk} η τιμή της συνάρτησης κλίσης στο xk και \textbf{xk} το σημείο ενδιαφέροντος. | |||
| Για την κάθε μία από αυτές δημιουργήσαμε ξεχωριστή συνάρτηση που υλοποιεί το παραπάνω interface. | |||
| Μία για σταθερό βήμα, μία για επιλογή βήματος που ελαχιστοποιεί την $f(x_k + \gamma_k d_k)$ και μία με τη μέθοδο Armijo. | |||
| Για την επιλογή και κλήση των μεθόδων επιλογής βήματος εισαγάγαμε μία νέα παράμετρο string που χρησιμοποιείται ως enumerator και με βάση αυτή γίνεται η τελική επιλογή. | |||
| @@ -134,8 +134,8 @@ | |||
| Η βασική ιδέα είναι ότι η συνάρτηση πρέπει να μειώνεται "αρκετά" σε κάθε βήμα, χωρίς να χρειάζεται να υπολογίζεται το ακριβές ελάχιστο. | |||
| Η συνθήκη του Armijo είναι: | |||
| \boldmath | |||
| \[ f(x_k + \gamma_k d_k) \leq f(x_k) + \sigma\gamma_k\nabla f(x_k)^Td_k\] | |||
| Όπου $\sigma \in (0,1)$ είναι μια σταθερά (τυπικά $\sigma = 0.1$) και $\gamma_k$ αρχικά να ορίζεται ως 1 και να μειώνεται προοδευτικά (π.χ., $\gamma_k = \beta \cdot \gamma_k$) έως ότου ικανοποιηθεί η συνθήκη. | |||
| \[ f(x_k + \gamma_k d_k) \leq f(x_k) + \sigma\gamma_k {d_k}^T*\nabla f(x_k) \] | |||
| Όπου $\sigma \in (0, 0.1)$ είναι μια σταθερά (τυπικά $\sigma = 0.1$) και $\gamma_k$ αρχικά να ορίζεται ως 1 και να μειώνεται προοδευτικά (π.χ., $\gamma_k = \beta \cdot \gamma_k$) έως ότου ικανοποιηθεί η συνθήκη. | |||
| \unboldmath | |||
| \par | |||
| Πλεονεκτήματα της μεθόδου είναι η \textbf{σταθερότητα}, καθώς αποτρέπει πολύ μεγάλα βήματα που μπορεί να αυξήσουν την τιμή της $f(x)$, αλλά και η \textbf{ανθεκτικότητα}, καθώς λειτουργεί καλά ακόμα και όταν η $f(x)$ δεν συμπεριφέρεται πολύ καλά. | |||
| @@ -157,25 +157,94 @@ | |||
| Για το σημείο (0, 0) η κλίση της $f$ είναι: $\nabla f(0,0) = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$, με αποτέλεσμα η μέθοδος να μην μπορεί να εφαρμοστεί για κανένα τρόπο υπολογισμού βήματος. | |||
| \subsection{Σημείο εκκίνησης (-1,1)} | |||
| Για το σημείο (-1, 1) η τιμή της $f$ είναι: $f(-1, 1) = -0.135335$ και η τιμή της κλίσης: $\nabla f(0,0) = \begin{bmatrix} 0.4060 \\ 0.2707 \end{bmatrix}$. | |||
| Επιλέγοντας ακρίβεια $\epsilon = 0.0001$, εκτελούμε την μέθοδο method\_steepest\_descent() και υπολογίζουμε τον αριθμό επαναλήψεων για διαφορετικές τιμές $\gamma_k$. | |||
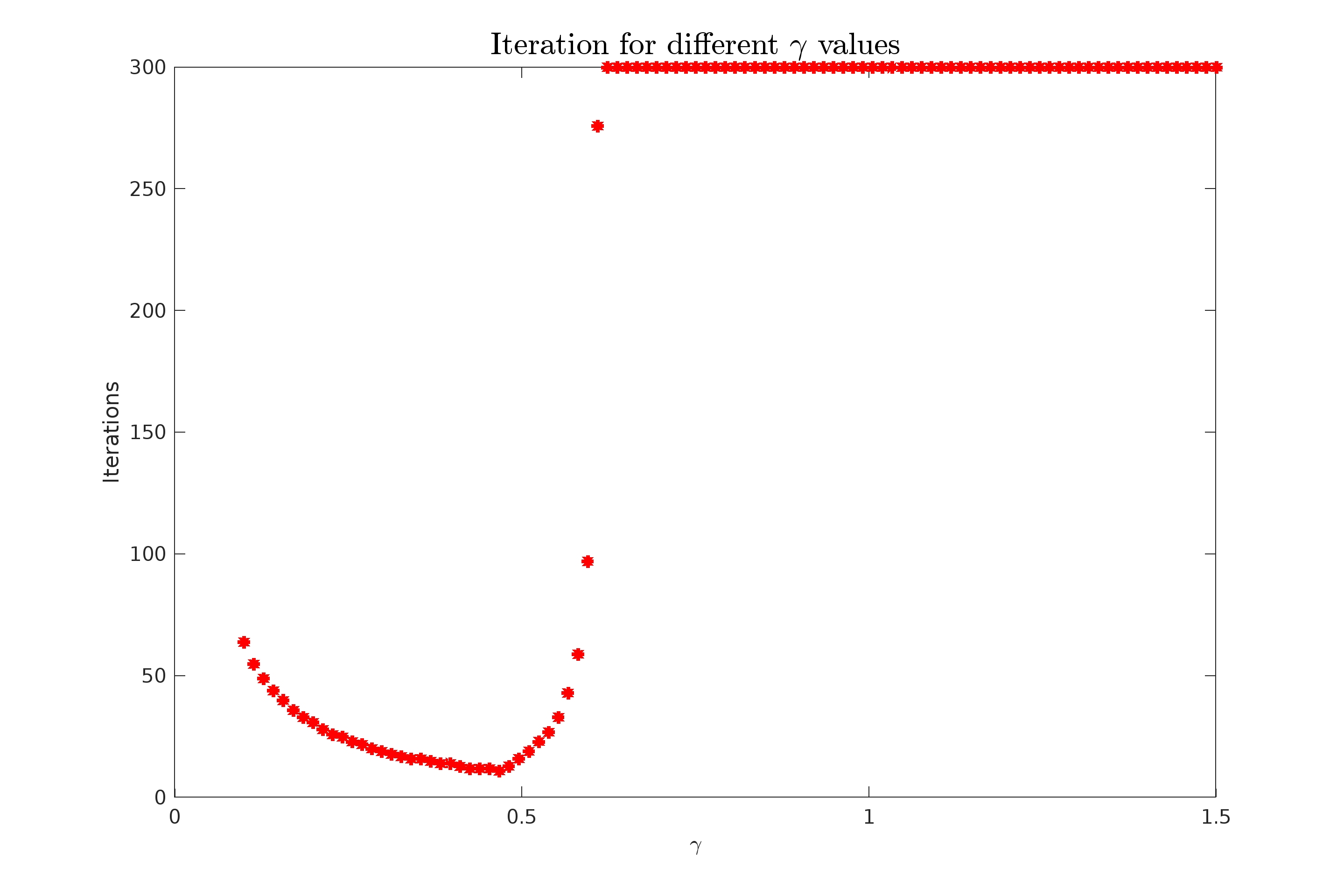
| \InsertFigure{H}{0.8}{fig:point2ItersOverGamma}{../scripts/figures/StDes_Iter_o_gamma_2.png}{Αριθμός επαναήψεων για διαφορετικές τιμές $\gamma_k [Μέγιστη Κάθοδος]$}. | |||
| Για το σημείο (-1, 1) η τιμή της $f$ είναι: $f(-1, 1) = -0.135335$ και το διάνυσμα της κλίσης: $\nabla f(0,0) = \begin{bmatrix} 0.4060 \\ 0.2707 \end{bmatrix}$, επομένως μπορούμε να εφαρμόσουμε τη μέθοδο. | |||
| \par | |||
| \underline{Σταθερό βήμα} \\ | |||
| Επιλέγοντας ακρίβεια $\epsilon = 0.0001$, εκτελούμε την μέθοδο \textit{method\_steepest\_descent()} και υπολογίζουμε τον αριθμό επαναλήψεων για διαφορετικές τιμές $\gamma_k$. | |||
| \InsertFigure{H}{0.8}{fig:point2ItersOverGamma}{../scripts/figures/StDes_Iter_o_gamma_2.png}{Αριθμός επαναλήψεων για διαφορετικές τιμές $\gamma_k$ [Μέγιστη Κάθοδος].} | |||
| Στο παραπάνω σχήμα \ref{fig:point2ItersOverGamma} παρατηρούμε ότι για τιμές του $\gamma_k > 0.61$ η μέθοδος αποκλίνει. | |||
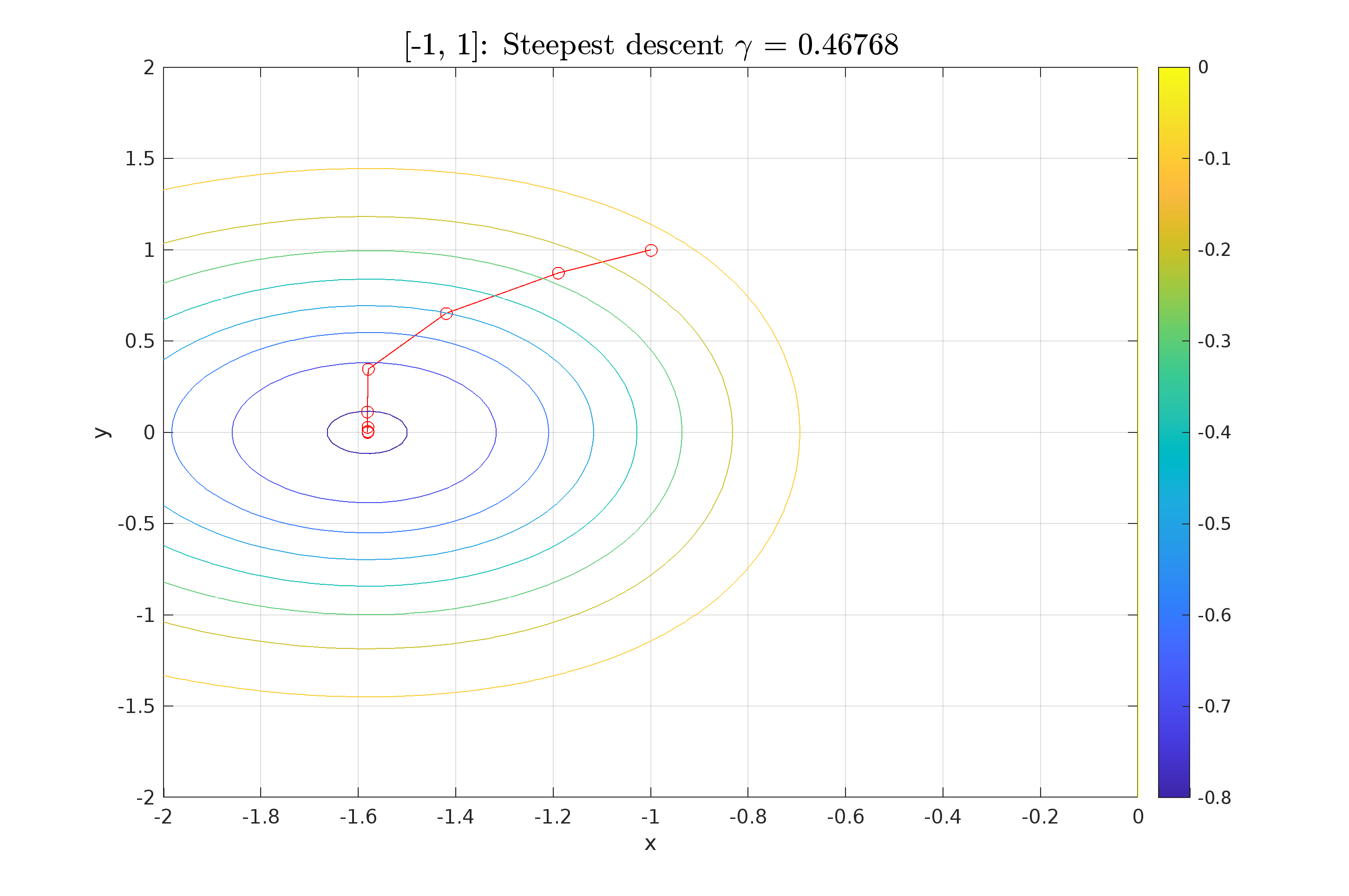
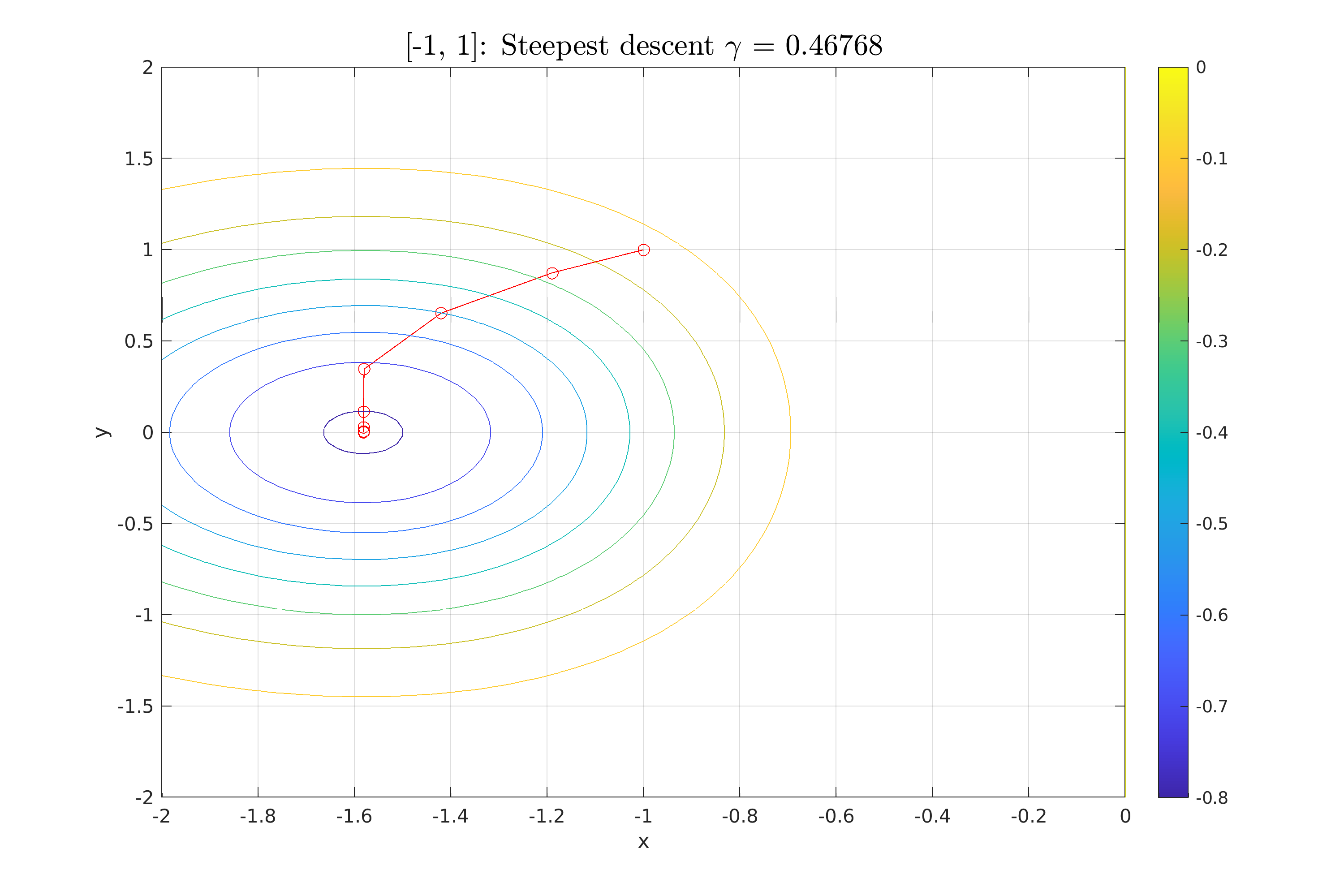
| Από την παραπάνω διαδικασία επίσης υπολογίζουμε το $\gamma_k = 0,46768$ για το οποίο η μέθοδος συγκλίνει με τα λιγότερα βήματα. | |||
| Στο παρακάτω σχήμα \ref{ref:StDes_fixed_2} | |||
| Στο παρακάτω σχήμα \ref{fig:StDes_fixed_2} αναπαριστούμε την πορεία των σημείων καθώς συγκλίνουν στο ελάχιστο. | |||
| \InsertFigure{H}{0.8}{fig:StDes_fixed_2}{../scripts/figures/StDes_fixed_2.png}{Σύγκλιση της μεθόδου Steepest descent [fixed $\gamma_k$].} | |||
| \par | |||
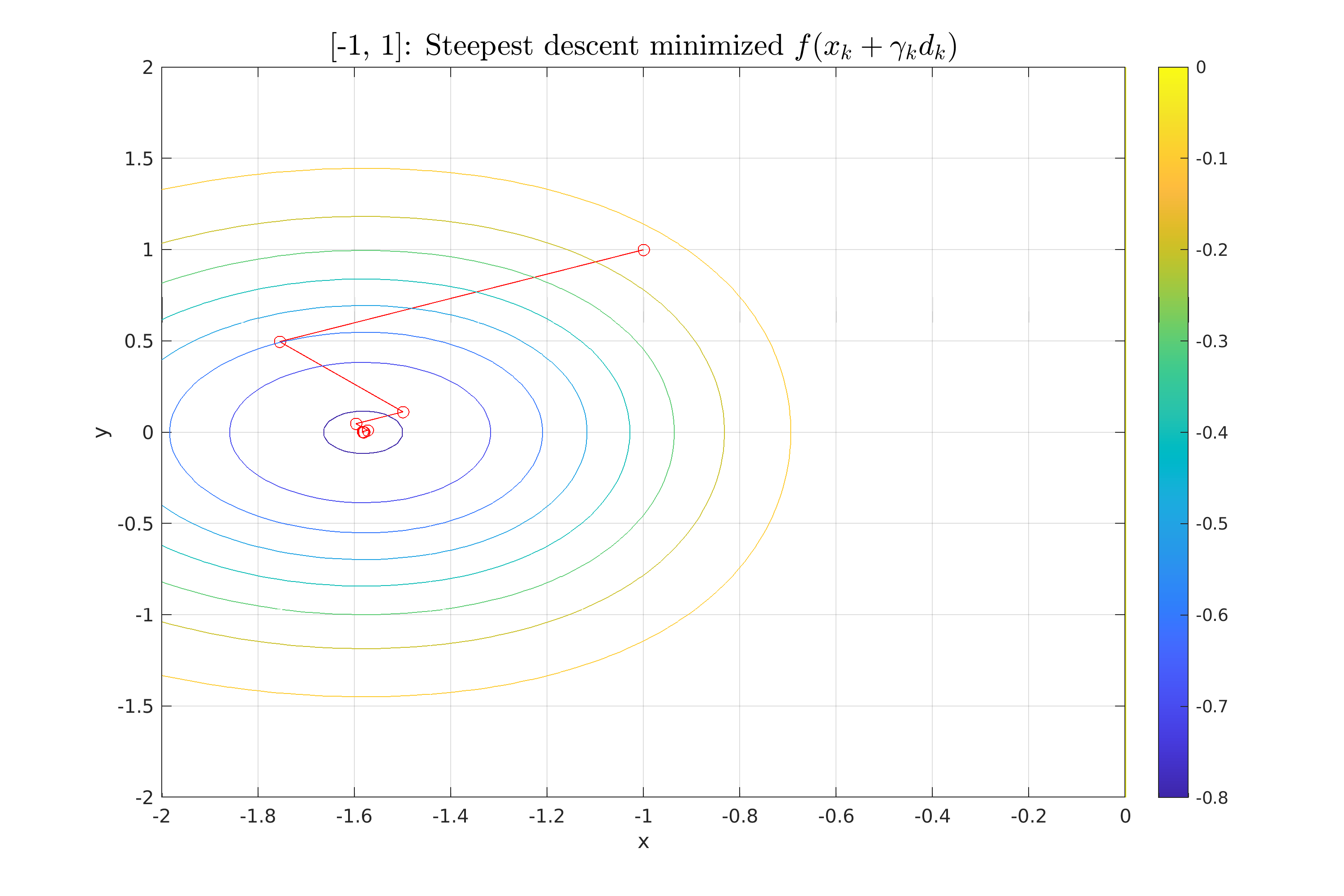
| \underline{Ελαχιστοποίηση της $f(x_k + \gamma_k d_k$)} \\ | |||
| Για την ελαχιστοποίηση της $f$, χρησιμοποιήθηκε η bisection από την προηγούμενη εργασία, η οποία τροποποιήθηκε ώστε δέχεται functions και όχι symbolic expressions. | |||
| \InsertFigure{H}{0.8}{fig:StDes_minimized_2}{../scripts/figures/StDes_minimized_2.png}{Σύγκλιση της μεθόδου Steepest descent [minimized f].} | |||
| Από το γράφημα φαίνεται τόσο ότι η μέθοδος συγκλίνει κοντά στο ελάχιστο γρηγορότερα, όσο και ότι πραγματοποιεί “διορθώσεις πορείας”. | |||
| \par | |||
| \underline{Armijo rule} \\ | |||
| Για τη μέθοδο η βασική ιδέα είναι να ξεκινήσει ο αλγόριθμος από ένα μεγάλο $\gamma_k = 1$ και συνεχώς να μειώνεται με βάση τον κανόνα Armijo. | |||
| Μετά από ένα tuning των παραμέτρων της μεθόδου καταλήξαμε στα $\beta=0.4, \sigma=0.1$ | |||
| \InsertFigure{H}{0.8}{fig:StDes_armijo_2}{../scripts/figures/StDes_armijo_2.png}{Σύγκλιση της μεθόδου Steepest descent [armijo rule].} | |||
| \InsertFigure{H}{0.8}{StDes_fixed_2}{../scripts/figures/StDes_fixed_2.png}{Σύγκλιση της μεθόδου}. | |||
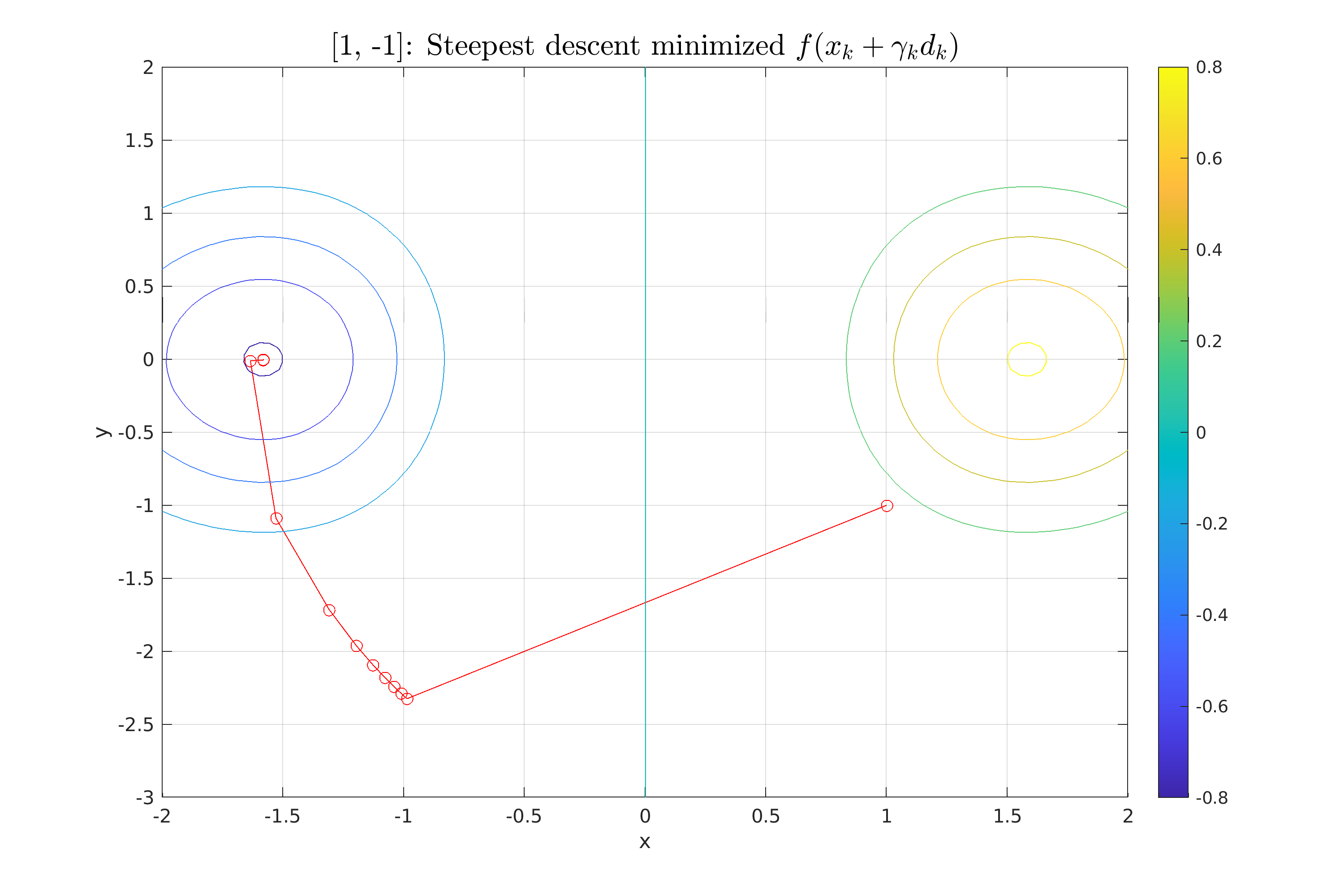
| \subsection{Σημείο εκκίνησης (1,-1)} | |||
| Για το σημείο (1, -1) η τιμή της $f$ είναι: $f(1, -1) = -0.135335$ και το διάνυσμα της κλίσης: $\nabla f(0,0) = \begin{bmatrix} 0.4060 \\ 0.2707 \end{bmatrix}$, επομένως μπορούμε να εφαρμόσουμε τη μέθοδο. | |||
| \par | |||
| \underline{Σταθερό βήμα} \\ | |||
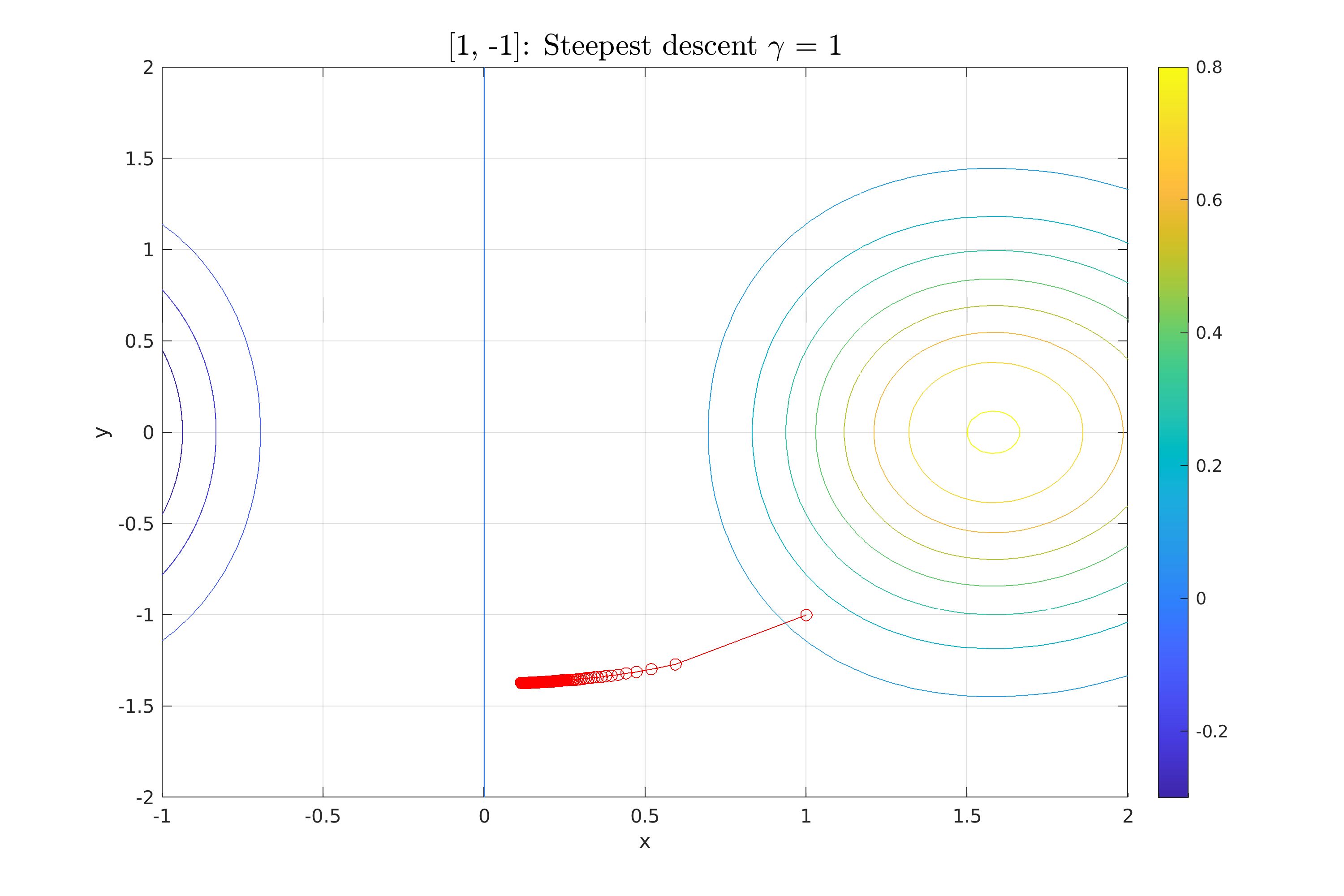
| Για σταθερό βήμα εκτελέσαμε διαδοχικά τη μέθοδο \textit{method\_steepest\_descent()} για να υπολογίσουμε τον αριθμό επαναλήψεων για διαφορετικές τιμές $\gamma_k$, όμως σε καμία τιμή ο αλγόριθμος δεν συγκλίνει. | |||
| Ακόμα και για μεγάλες τιμές του $\gamma_k$, ο αλγόριθμος εγκλωβίζεται στο δεξιό ημιεπίπεδο. | |||
| \InsertFigure{H}{0.8}{fig:StDes_fixed_3}{../scripts/figures/StDes_fixed_3.png}{Μη σύγκλιση της μεθόδου Steepest descent [Fixed step].} | |||
| \par | |||
| \underline{Ελαχιστοποίηση της $f(x_k + \gamma_k d_k$)} \\ | |||
| \InsertFigure{H}{0.8}{fig:StDes_minimized_3}{../scripts/figures/StDes_minimized_3.png}{Σύγκλιση της μεθόδου Steepest descent [minimized f].} | |||
| Από το γράφημα φαίνεται ότι η μέθοδος συγκλίνει, καταφέρνοντας να περάσει την περιοχή με μηδενικές κλίσεις κοντά στον άξονα των $\psi$. | |||
| \par | |||
| \underline{Armijo rule} \\ | |||
| \InsertFigure{H}{0.8}{fig:StDes_armijo_3}{../scripts/figures/StDes_armijo_3.png}{Μη σύγκλιση της μεθόδου Steepest descent [armijo rule].} | |||
| Αντίθετα η μέθοδος armijo δεν συγκλίνει, καθώς εγκλωβίζεται στο δεξιό ημιεπίπεδο. | |||
| \section{Μέθοδος Newton} | |||
| Η δεύτερη μέθοδος που χρησιμοποιούμε στην εργασία (Θέμα 3), είναι η μέθοδος Newton. | |||
| Η μέθοδος χρησιμοποιεί πληροφορίες δεύτερης τάξης (Hessian) για τη βελτίωση της κατεύθυνσης καθόδου. | |||
| Αν η συνάρτηση είναι τετραγωνική, η μέθοδος συγκλίνει σε ένα βήμα. | |||
| Η μέθοδος ορίζει την κατεύθυνση | |||
| \boldmath\[d_k = -{H_k}^{-1}\nabla f(x_k)\]\unboldmath | |||
| Όπου $H_k$ είναι ο Εσσιανός πίνακας της $f$ στο $x_k$. | |||
| Το επόμενο σημείο υπολογίζεται ως | |||
| \boldmath\[x_{k+1} = x_k + \gamma_k d_k\]\unboldmath | |||
| Με κατάλληλο υπολογισμό του βήματος. | |||
| Για να λειτουργήσει η μέθοδος η $f$ πρέπει να είναι \textbf{δύο φορές διαφορίσιμη} και ο Εσσιανός \boldmath$H_k$\unboldmath να είναι \textbf{θετικά ορισμένος και αντιστρέψιμος}. | |||
| \par | |||
| Στα πλεονεκτήματα της μεθόδου είναι η \textbf{ταχύτερη σύγκλιση} από την Steepest Descent για κυρτές συναρτήσεις και το γεγονός ότι εκμεταλλεύεται την \textbf{πληροφορία καμπυλότητας} της συνάρτησης. | |||
| Όμως είναι υπολογιστικά δαπανηρή και δεν είναι ανθεκτική σε μη κυρτές συναρτήσεις ή σε περιπτώσεις όπου ο Εσσιανός είναι κακώς ορισμένος. | |||
| Όλοι οι υπολογισμοί για τη μέθοδο βρίσκονται στο αρχείο \textbf{Script\_3\_Newton.m} | |||
| \subsection{Σημείο εκκίνησης (0,0)} | |||
| Για το σημείο $x_k = (0, 0)$ η κλίση της $f$ είναι: $\nabla f(x_k) = \begin{bmatrix} 0 \\ 0 \end{bmatrix}$ και ο εσσιανός $H(x_k) = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$ με αποτέλεσμα η μέθοδος και εδώ να μην μπορεί να εφαρμοστεί για κανένα τρόπο υπολογισμού βήματος. | |||
| \subsection{Σημείο εκκίνησης (-1,1)} | |||
| Για το σημείο $x_k = (-1, 1)$ η κλίση της $f$ είναι: $\nabla f(x_k) = \begin{bmatrix} 0.406 \\ 0.270 \end{bmatrix}$ και ο εσσιανός $H(x_k) = \begin{bmatrix} -0.270 & -0.812 \\ -0.812 & -0.270 \end{bmatrix}$ με ιδιοτιμές $\lambda = \begin{bmatrix} -1.082 \\ 0.541 \end{bmatrix}$. | |||
| Από τα παραπάνω προκύπτει πως ο Εσσιανός είναι αόριστος και άρα δεν μπορεί να εφαρμοστεί η μέθοδος, για κανένα τρόπο υπολογισμού βήματος. | |||
| \subsection{Σημείο εκκίνησης (1,-1)} | |||
| Για το σημείο $x_k = (1, -1)$ η κλίση της $f$ είναι: $\nabla f(x_k) = \begin{bmatrix} 0.406 \\ 0.270 \end{bmatrix}$ και ο εσσιανός $H(x_k) = \begin{bmatrix} 0.270 & 0.812 \\ 0.812 & 0.270 \end{bmatrix}$ με ιδιοτιμές $\lambda = \begin{bmatrix} -0.541 \\ 1.082 \end{bmatrix}$. | |||
| Και εδώ, από τα παραπάνω προκύπτει πως ο Εσσιανός είναι αόριστος και άρα δεν μπορεί να εφαρμοστεί η μέθοδος, για κανένα τρόπο υπολογισμού βήματος. | |||
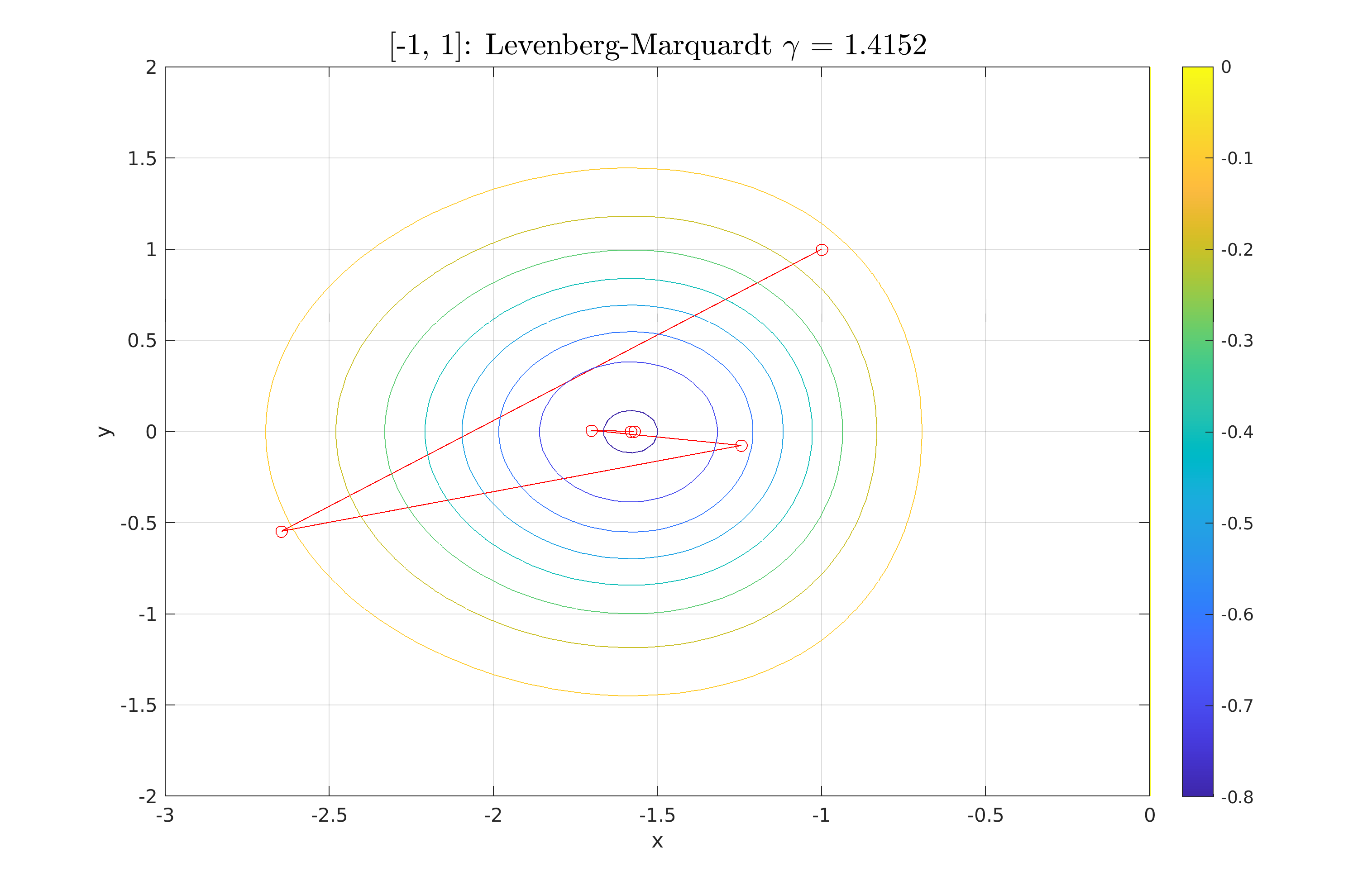
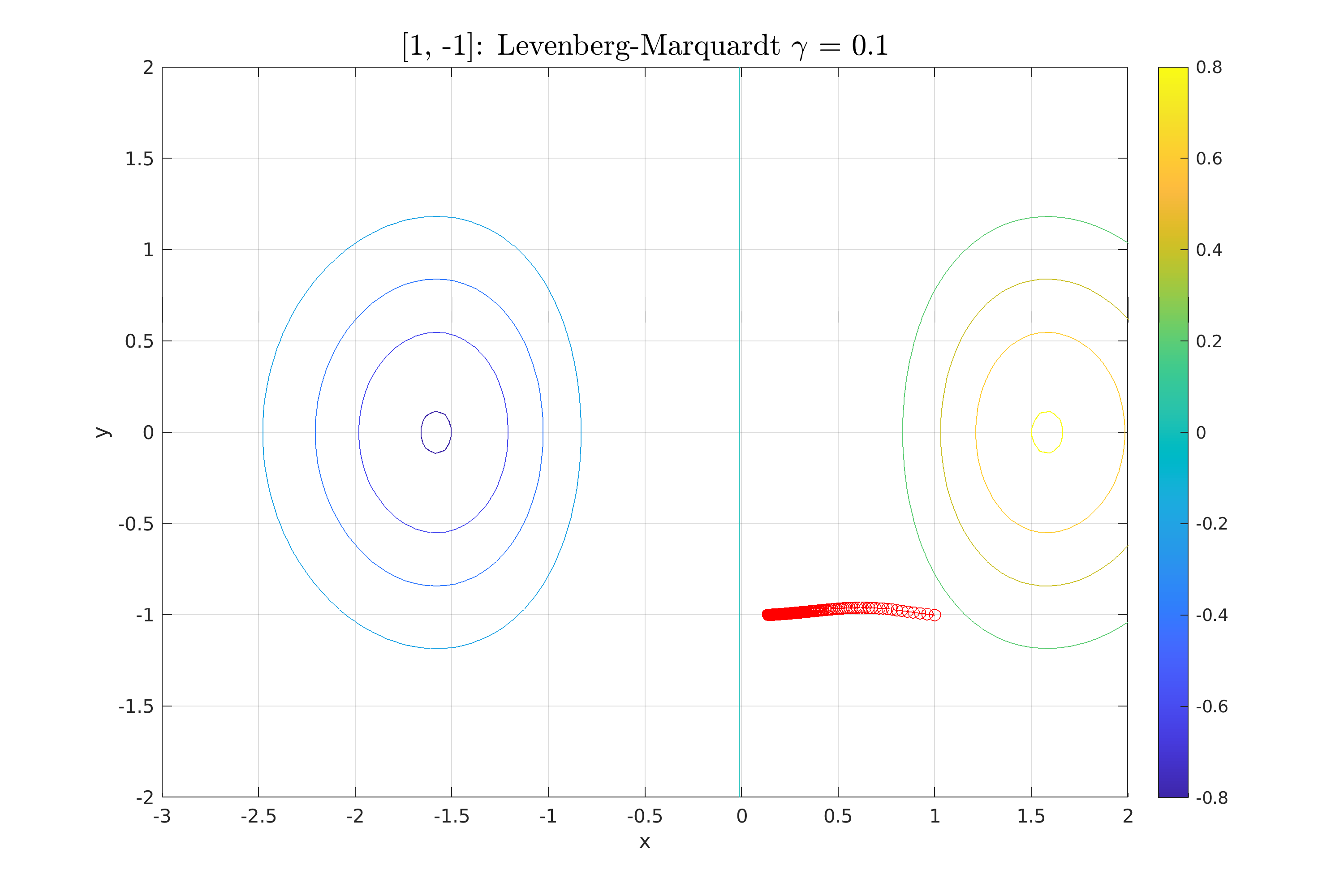
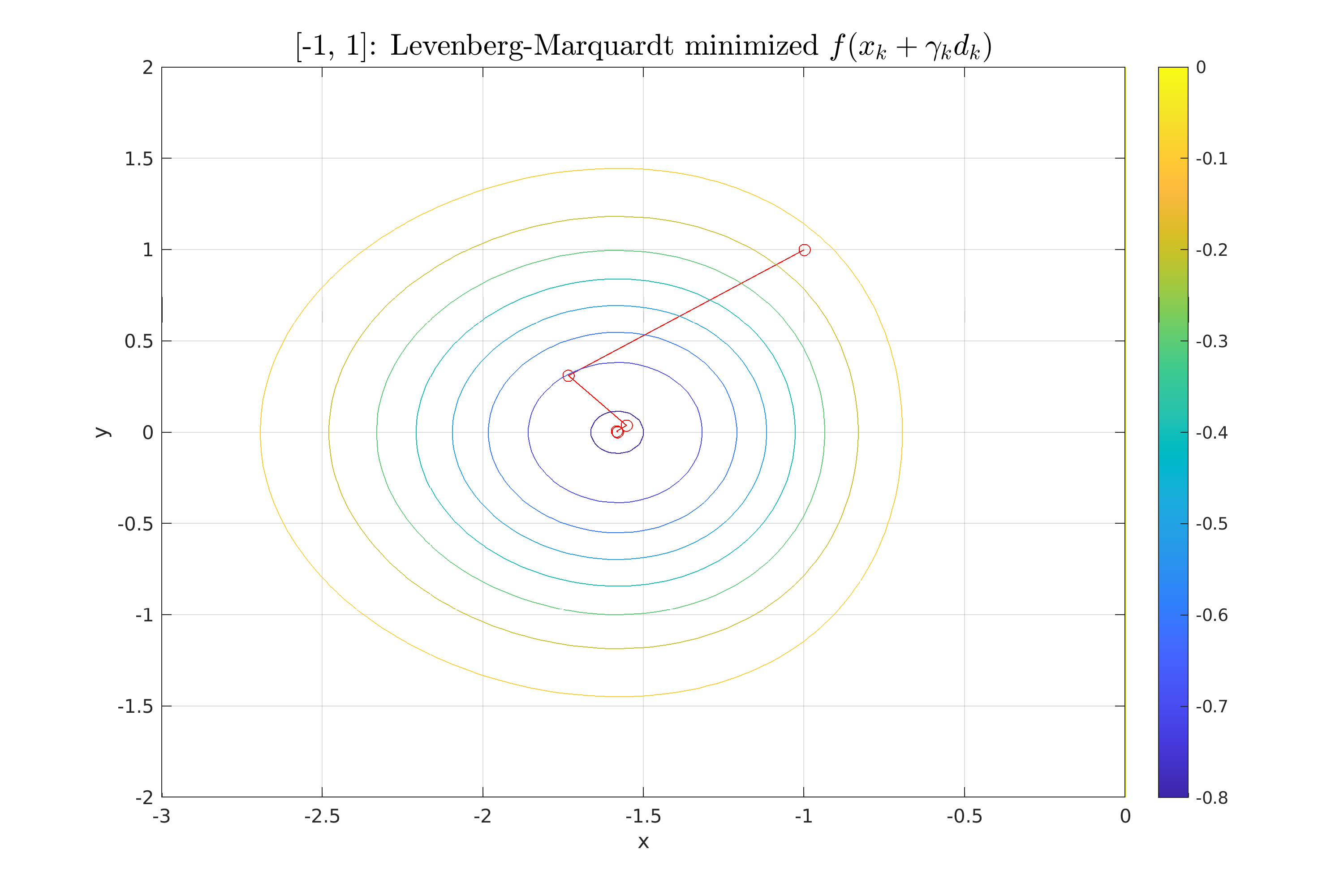
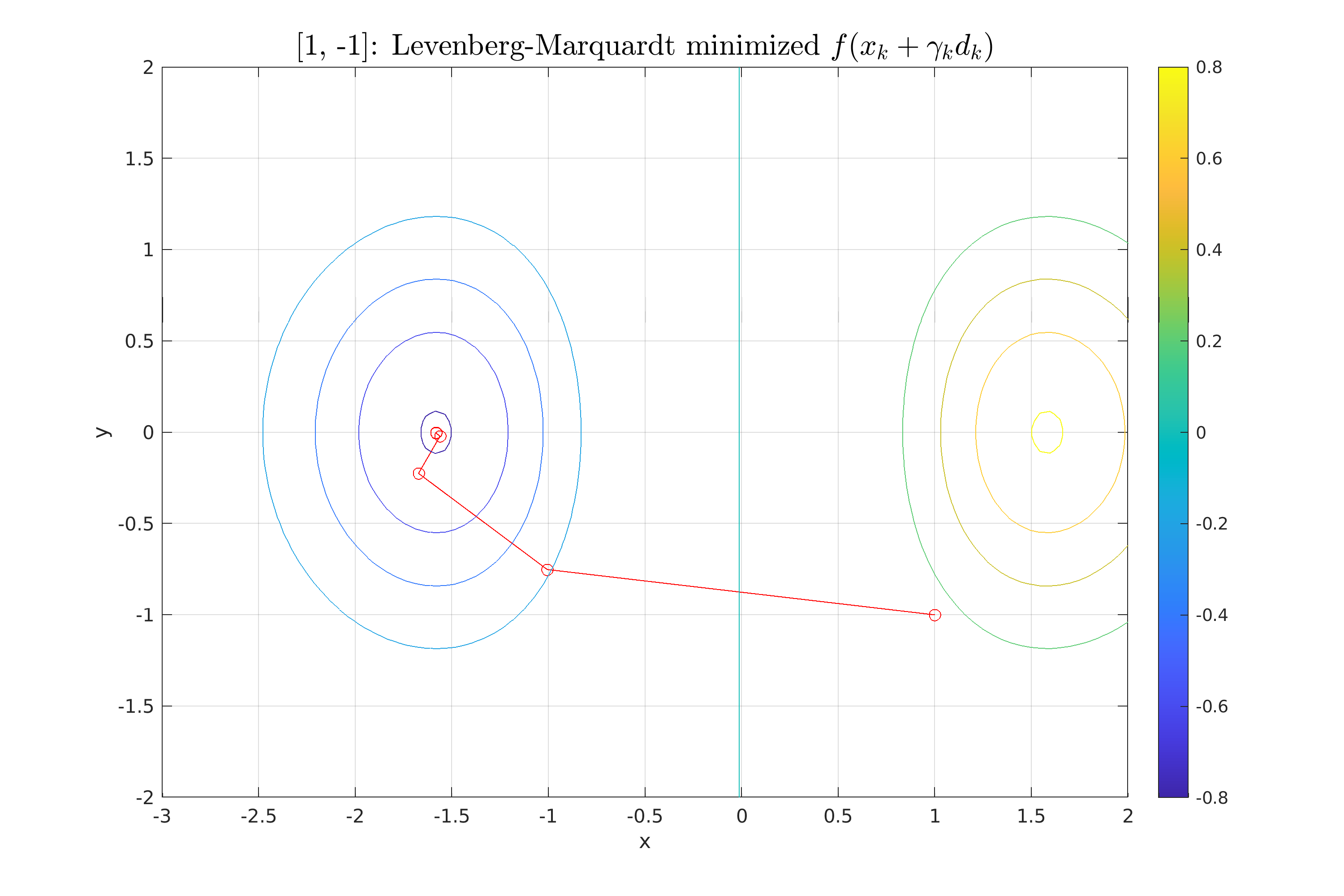
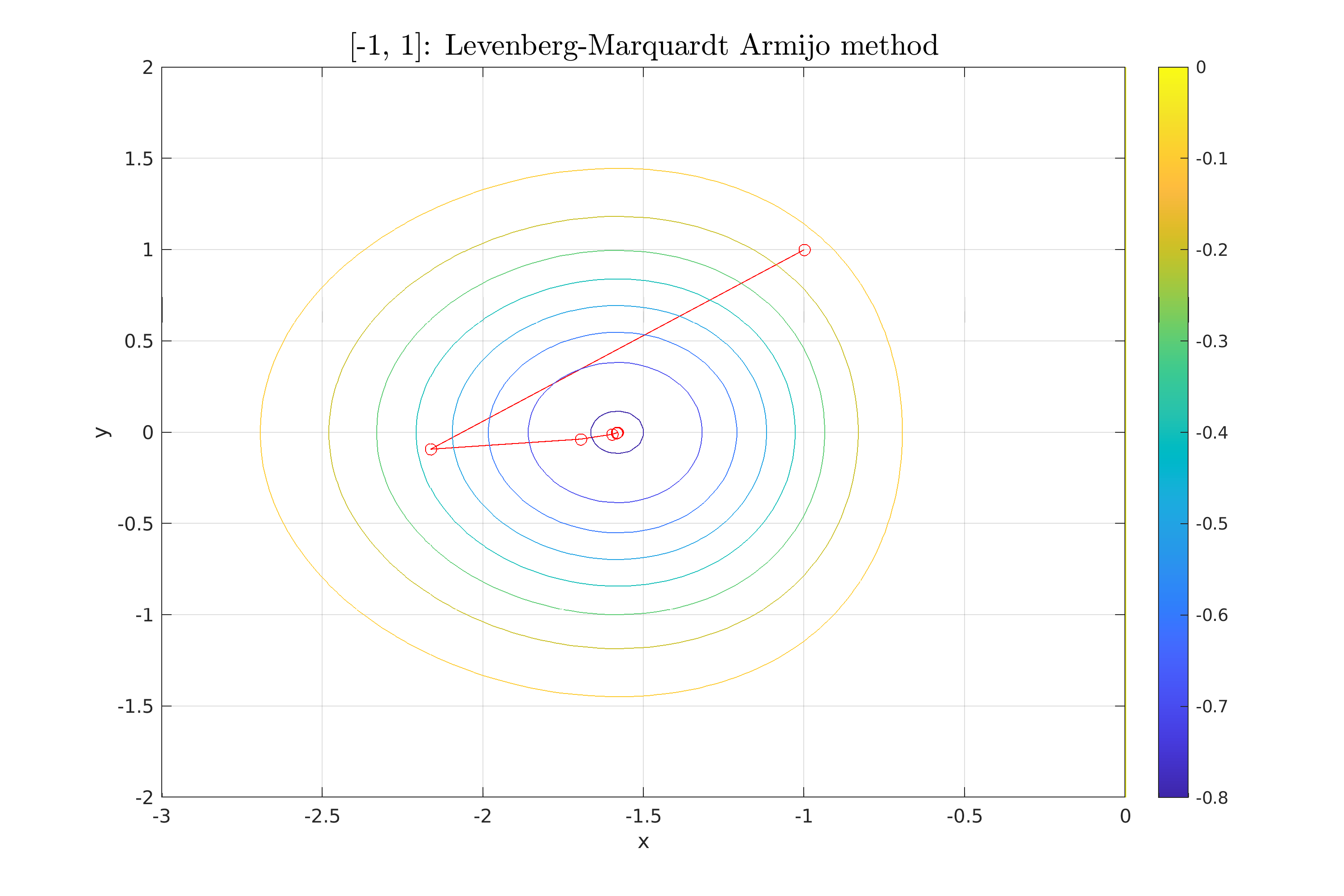
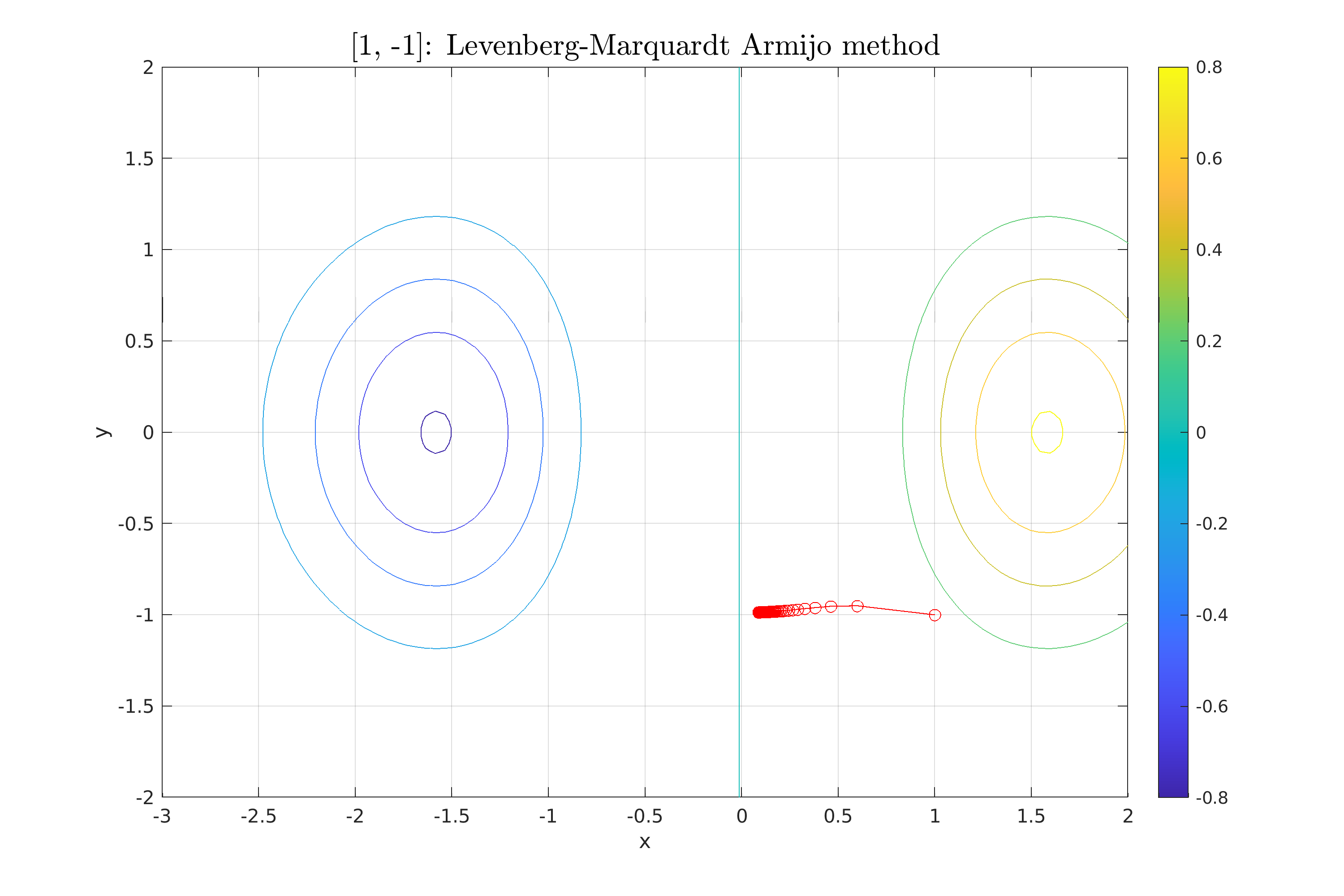
| \section{Μέθοδος Levenberg-Marquardt} | |||
| Η τελευταία μέθοδος που χρησιμοποιούμε στην εργασία (Θέμα 4), είναι η μέθοδος Levenberg-Marquardt. | |||
| Πρόκειται για μια τροποποιημένη έκδοση της μεθόδου Newton, η οποία εισάγει έναν παράγοντα απόσβεσης για τη σταθεροποίηση όταν ο εσσιανός δεν είναι θετικά ορισμένος. | |||
| Για το λόγο αυτό χρησιμοποιεί ένας προσαρμοσμένος εσσιανός $H_k' = H_k + \mu_k I$, όπου $\mu_k > 0$ ένας παράγοντας απόσβεσης. | |||
| Για μεγάλες τιμές του $\mu_k$ η μέθοδος συμπεριφέρεται σαν Gradient Descent. | |||
| %Απαιτήσεις: | |||
| %Η f(x)f(x) πρέπει να είναι δύο φορές διαφορίσιμη. | |||
| %Υπολογισμός του λλ απαιτεί προσεκτική επιλογή παραμέτρων. | |||
| %Περιορισμοί: | |||
| %Η απόδοση εξαρτάται από την επιλογή του αρχικού λλ. | |||
| %Μπορεί να παρουσιάσει αργή σύγκλιση σε προβλήματα χωρίς κυρτότητα. | |||
| %Πλεονεκτήματα: | |||
| %Σταθερή ακόμη και για κακώς ορισμένα Hessians. | |||
| %Λειτουργεί καλά σε προβλήματα που συνδυάζουν γραμμικές και μη γραμμικές εξαρτήσεις. | |||
| %Μειονεκτήματα: | |||
| %Υψηλότερο υπολογιστικό κόστος σε σχέση με το Steepest Descent. | |||
| Όλοι οι υπολογισμοί για τη μέθοδο βρίσκονται στο αρχείο \textbf{Script\_4\_LevMar.m} | |||
| \section{Σύγκριση των μεθόδων} | |||
| Εκτελώντας όλους του αλγόριθμους για τα ίδια δεδομένα, \textbf{για τον αριθμό επαναλήψεων} έχουμε: \\ | |||
| \par | |||
| \underline{Παρατηρήσεις:} | |||
| \begin{itemize} | |||
| \item ... | |||
| \end{itemize} | |||
+ 2
- 1
Work2/scripts/GivenEnv.m
Dosyayı Görüntüle
| @@ -16,7 +16,8 @@ grad_fun = matlabFunction(grad_fexpr, 'Vars', [x, y]); % Gradient | |||
| hessian_fun = matlabFunction(hessian_fexpr, 'Vars', [x, y]); % Hessian | |||
| % Amijo globals | |||
| global amijo_beta amijo_sigma | |||
| global amijo_beta; % Step reduction factor in [0.1, 0.5] (typical range: [0.1, 0.8]) | |||
| global amijo_sigma; % Sufficient decrease constant in [1e-5, 0.1] (typical range: [0.01, 0.3]) | |||
| %fixed step size globals | |||
| global gamma_fixed_step | |||
+ 67
- 15
Work2/scripts/Script_2_Steepest_descent.m
Dosyayı Görüntüle
| @@ -5,22 +5,19 @@ GivenEnv | |||
| max_iter = 300; % Maximum iterations | |||
| tol = 1e-4; % Tolerance | |||
| % Methods tuning | |||
| amijo_beta = 0.5; % Armijo reduction factor | |||
| amijo_sigma = 0.1; % Armijo condition constant | |||
| % Point x0 = (0, 0) | |||
| % ========================================================================= | |||
| point = 1; | |||
| x0 = [0, 0]; | |||
| f = fun(x0(1), x0(2)); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Can not use method\n\n', x0, f, gf, hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Can NOT use method\n', x0, f, gf, hf); | |||
| disp(' '); | |||
| % Points x0 = (-1, 1), (1, -1) | |||
| %x0s = [-1, 1 ; 1, -1]; % Initial points | |||
| % Point x0 = (-1, 1) | |||
| % ========================================================================= | |||
| point = 2; | |||
| x0 = [-1, 1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| @@ -49,14 +46,69 @@ fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), | |||
| plotPointsOverContour(x_fixed, fun, [-2, 0], [-2, 2], 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, "figures/StDes_fixed_" + point + ".png"); | |||
| % Minimized f | |||
| [x_minimized, f_minimized, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_minimized(end, :), f_minimized(end)); | |||
| plotPointsOverContour(x_minimized, fun, [-2, 2], [-2, 2], 100, point_str + ": Steepest descent minimized $f(x_k + \gamma_kd_k)$", "StDes_minimized_" + i + ".png"); | |||
| % Minimized f | |||
| [x_minimized, f_minimized, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_minimized(end, :), f_minimized(end)); | |||
| plotPointsOverContour(x_minimized, fun, [-2, 0], [-2, 2], 100, point_str + ": Steepest descent minimized $f(x_k + \gamma_kd_k)$", "figures/StDes_minimized_" + point + ".png"); | |||
| % Armijo Rule | |||
| % Methods tuning | |||
| amijo_beta = 0.4; % typical range: [0.1, 0.8] | |||
| amijo_sigma = 0.1; % typical range: [0.01, 0.3] | |||
| [x_armijo, f_armijo, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-2, 0], [-2, 2], 100, point_str + ": Steepest descent Armijo method", "figures/StDes_armijo_" + point + ".png"); | |||
| disp(' '); | |||
| % Point x0 = (1, -1) | |||
| % ========================================================================= | |||
| point = 3; | |||
| x0 = [1, -1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| f = fun(-1, 1); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Can use method\n', x0, f, gf, hf); | |||
| % Find the best fixed gamma | |||
| k = zeros(100, 1); | |||
| j = 1; | |||
| n = linspace(0.1, 1, 100); | |||
| for g = n | |||
| gamma_fixed_step = g; | |||
| [~, ~, k(j)] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'fixed'); | |||
| j = j + 1; | |||
| end | |||
| %if min(k) == max_iter | |||
| % fprintf('Fixed step: Initial point (%d, %d). Can NOT use method\n', x0); | |||
| %end | |||
| %plotItersOverGamma(n, k, "Iteration for different $\gamma$ values", "figures/StDes_Iter_o_gamma_" + point + ".png"); | |||
| %gamma_fixed_step = 1; | |||
| [x_fixed, f_fixed, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'fixed'); | |||
| fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-1, 2], [-2, 2], 100, point_str + ": Steepest descent $\gamma$ = " + gamma_fixed_step, "figures/StDes_fixed_" + point + ".png"); | |||
| % Minimized f | |||
| [x_minimized, f_minimized, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_minimized(end, :), f_minimized(end)); | |||
| plotPointsOverContour(x_minimized, fun, [-2, 2], [-3, 2], 100, point_str + ": Steepest descent minimized $f(x_k + \gamma_kd_k)$", "figures/StDes_minimized_" + point + ".png"); | |||
| % Armijo Rule | |||
| % Methods tuning | |||
| amijo_beta = 0.4; % typical range: [0.1, 0.8] | |||
| amijo_sigma = 0.1; % typical range: [0.01, 0.3] | |||
| [x_armijo, f_armijo, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-1, 2], [-2, 2], 100, point_str + ": Steepest descent Armijo method", "figures/StDes_armijo_" + point + ".png"); | |||
| % Armijo Rule | |||
| [x_armijo, f_armijo, kk] = method_steepest_descent(fun, grad_fun, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-2, 2], [-2, 2], 100, point_str + ": Steepest descent Armijo method", "StDes_armijo_" + i + ".png"); | |||
+ 36
- 44
Work2/scripts/Script_3_Newton.m
Dosyayı Görüntüle
| @@ -1,51 +1,43 @@ | |||
| % Define environment (functions, gradients etc...) | |||
| GivenEnv | |||
| % Define parameters | |||
| max_iter = 300; % Maximum iterations | |||
| tol = 1e-4; % Tolerance | |||
| % Methods tuning | |||
| amijo_beta = 0.5; % Armijo reduction factor | |||
| amijo_sigma = 0.1; % Armijo condition constant | |||
| % Point x0 = (0, 0) | |||
| % x0 = [0, 0]; | |||
| % ========================================================================= | |||
| point = 1; | |||
| x0 = [0, 0]; | |||
| f = fun(x0(1), x0(2)); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can NOT use method\n', x0, f, gf, hf, ev); | |||
| disp(' '); | |||
| % Point x0 = (-1, 1) | |||
| % ========================================================================= | |||
| point = 2; | |||
| x0 = [-1, 1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| f = fun(-1, 1); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can NOT use method\n', x0, f, gf, hf, ev); | |||
| disp(' '); | |||
| % Point x0 = (1, -1) | |||
| % ========================================================================= | |||
| point = 3; | |||
| x0 = [1, -1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| f = fun(-1, 1); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can NOT use method\n', x0, f, gf, hf, ev); | |||
| % Point x0 = (0, 0) | |||
| x0s = [0, 0; -1, 1 ; 1, -1]; % Initial points | |||
| for i = 1:size(x0s, 1) | |||
| x0 = x0s(i, :); | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| % Find the best fixed gamma | |||
| k = zeros(100, 1); | |||
| j = 1; | |||
| n = linspace(0.1, 1.5, 100); | |||
| for g = n | |||
| gamma_fixed_step = g; | |||
| [~, ~, k(j)] = newton(fun, grad_fun, hessian_fun, x0, tol, max_iter, 'fixed'); | |||
| j = j + 1; | |||
| end | |||
| plotIterationsOverGamma(n, k, "Iteration for different $\gamma$ values", "Newton_Iter_o_gamma_" + i + ".png"); | |||
| [~, j] = min(k); | |||
| gamma_fixed_step = n(j); | |||
| [x_fixed, f_fixed, kk] = newton(fun, grad_fun, hessian_fun, x0, tol, max_iter, 'fixed'); | |||
| fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-2, 2], [-3, 3], 100, point_str + ": Newton $\gamma$ = " + gamma_fixed_step, "Newton_fixed_" + i + ".png"); | |||
| % Minimized f | |||
| [x_minimized, f_minimized, kk] = newton(fun, grad_fun, hessian_fun, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_minimized(end, :), f_minimized(end)); | |||
| plotPointsOverContour(x_minimized, fun, [-2, 2], [-3, 3], 100, point_str + ": Newton minimized $f(x_k + \gamma_kd_k)$", "Newton_minimized_" + i + ".png"); | |||
| % Armijo Rule | |||
| [x_armijo, f_armijo, kk] = newton(fun, grad_fun, hessian_fun, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-2, 2], [-3, 3], 100, point_str + ": Newton Armijo method", "Newton_armijo_" + i + ".png"); | |||
| end | |||
+ 97
- 34
Work2/scripts/Script_4_LevMar.m
Dosyayı Görüntüle
| @@ -5,49 +5,112 @@ GivenEnv | |||
| max_iter = 300; % Maximum iterations | |||
| tol = 1e-4; % Tolerance | |||
| % Methods tuning | |||
| amijo_beta = 0.5; % Armijo reduction factor | |||
| amijo_sigma = 0.1; % Armijo condition constant | |||
| m = 0.01; | |||
| % Point x0 = (0, 0) | |||
| % x0 = [0, 0]; | |||
| % ========================================================================= | |||
| point = 1; | |||
| x0 = [0, 0]; | |||
| f = fun(x0(1), x0(2)); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can NOT use method\n', x0, f, gf, hf, ev); | |||
| disp(' '); | |||
| % Point x0 = (0, 0) | |||
| x0s = [0, 0; -1, 1 ; 1, -1]; % Initial points | |||
| for i = 1:size(x0s, 1) | |||
| x0 = x0s(i, :); | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| % Find the best fixed gamma | |||
| k = zeros(100, 1); | |||
| j = 1; | |||
| n = linspace(0.1, 1.5, 100); | |||
| for g = n | |||
| gamma_fixed_step = g; | |||
| [~, ~, k(j)] = lev_mar(fun, grad_fun, hessian_fun, m, x0, tol, max_iter, 'fixed'); | |||
| j = j + 1; | |||
| % Point x0 = (-1, 1) | |||
| % ========================================================================= | |||
| point = 2; | |||
| x0 = [-1, 1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| f = fun(-1, 1); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can use method\n', x0, f, gf, hf, ev); | |||
| % Find the best fixed gamma | |||
| k = zeros(100, 1); | |||
| j = 1; | |||
| n = linspace(0.1, 1.5, 100); | |||
| for g = n | |||
| gamma_fixed_step = g; | |||
| [x, f, k(j)] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'fixed'); | |||
| if ~(x(end, 1) < -1.57 && x(end, 1) > -1.59 && x(end, 2) < 0.01 && x(end,2) > -0.01 && f(end) < -0.8 && f(end) > -0.82) | |||
| k(j) = 300; | |||
| end | |||
| plotIterationsOverGamma(n, k, "Iteration for different $\gamma$ values", "LevMar_Iter_o_gamma_" + i + ".png"); | |||
| j = j + 1; | |||
| end | |||
| [~, j] = min(k); | |||
| gamma_fixed_step = n(j); | |||
| [x_fixed, f_fixed, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'fixed'); | |||
| fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-3, 0], [-2, 2], 100, point_str + ": Levenberg-Marquardt $\gamma$ = " + gamma_fixed_step, "figures/LevMar_fixed_" + point + ".png"); | |||
| [~, j] = min(k); | |||
| gamma_fixed_step = n(j); | |||
| [x_fixed, f_fixed, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-3, 0], [-2, 2], 100, point_str + ": Levenberg-Marquardt minimized $f(x_k + \gamma_kd_k)$", "figures/LevMar_minimized_" + point + ".png"); | |||
| [x_fixed, f_fixed, kk] = lev_mar(fun, grad_fun, hessian_fun, m, x0, tol, max_iter, 'fixed'); | |||
| fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-2, 2], [-3, 3], 100, point_str + ": LevMar $\gamma$ = " + gamma_fixed_step, "LevMar_fixed_" + i + ".png"); | |||
| % Armijo Rule | |||
| % Methods tuning | |||
| amijo_beta = 0.4; % typical range: [0.1, 0.8] | |||
| amijo_sigma = 0.1; % typical range: [0.01, 0.3] | |||
| [x_armijo, f_armijo, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-3, 0], [-2, 2], 100, point_str + ": Levenberg-Marquardt Armijo method", "figures/StDes_armijo_" + point + ".png"); | |||
| disp(' '); | |||
| % Minimized f | |||
| [x_minimized, f_minimized, kk] = lev_mar(fun, grad_fun, hessian_fun, m, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_minimized(end, :), f_minimized(end)); | |||
| plotPointsOverContour(x_minimized, fun, [-2, 2], [-3, 3], 100, point_str + ": LevMar minimized $f(x_k + \gamma_kd_k)$", "LevMar_minimized_" + i + ".png"); | |||
| % Point x0 = (1, -1) | |||
| % ========================================================================= | |||
| point = 3; | |||
| x0 = [1, -1]; | |||
| point_str = "[" + x0(1) + ", " + x0(2) + "]"; | |||
| % Armijo Rule | |||
| [x_armijo, f_armijo, kk] = lev_mar(fun, grad_fun, hessian_fun, m, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-2, 2], [-3, 3], 100, point_str + ": LevMar Armijo method", "LevMar_armijo_" + i + ".png"); | |||
| f = fun(-1, 1); | |||
| gf = grad_fun(x0(1), x0(2)); | |||
| hf = hessian_fun(x0(1), x0(2)); | |||
| ev = eig(hf); | |||
| fprintf('Initial point (%d, %d), f = %f, grad = [%f;%f], hessian = [%f %f ; %f %f]. Eigenvalues= [%f, %f], Can use method\n', x0, f, gf, hf, ev); | |||
| % Find the best fixed gamma | |||
| k = zeros(100, 1); | |||
| j = 1; | |||
| n = linspace(0.1, 1.5, 100); | |||
| for g = n | |||
| gamma_fixed_step = g; | |||
| [x, f, k(j)] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'fixed'); | |||
| if ~(x(end, 1) < -1.57 && x(end, 1) > -1.59 && x(end, 2) < 0.01 && x(end,2) > -0.01 && f(end) < -0.8 && f(end) > -0.82) | |||
| k(j) = 300; | |||
| end | |||
| j = j + 1; | |||
| end | |||
| [~, j] = min(k); | |||
| gamma_fixed_step = n(j); | |||
| [x_fixed, f_fixed, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'fixed'); | |||
| fprintf('Fixed step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-3, 2], [-2, 2], 100, point_str + ": Levenberg-Marquardt $\gamma$ = " + gamma_fixed_step, "figures/LevMar_fixed_" + point + ".png"); | |||
| [x_fixed, f_fixed, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'minimized'); | |||
| fprintf('Minimized f(g): Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_fixed(end, :), f_fixed(end)); | |||
| plotPointsOverContour(x_fixed, fun, [-3, 2], [-2, 2], 100, point_str + ": Levenberg-Marquardt minimized $f(x_k + \gamma_kd_k)$", "figures/LevMar_minimized_" + point + ".png"); | |||
| % Armijo Rule | |||
| % Methods tuning | |||
| amijo_beta = 0.4; % typical range: [0.1, 0.8] | |||
| amijo_sigma = 0.1; % typical range: [0.01, 0.3] | |||
| [x_armijo, f_armijo, kk] = method_lev_mar(fun, grad_fun, hessian_fun, 0.3, x0, tol, max_iter, 'armijo'); | |||
| fprintf('Armijo step: Initial point (%f, %f), steps:%d, Final (x,y)=(%f, %f), f(x,y)=%f\n', x0, kk, x_armijo(end, :), f_armijo(end)); | |||
| plotPointsOverContour(x_armijo, fun, [-3, 2], [-2, 2], 100, point_str + ": Levenberg-Marquardt Armijo method", "figures/StDes_armijo_" + point + ".png"); | |||
| disp(' '); | |||
BIN
Work2/scripts/figures/LevMar_fixed_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/LevMar_fixed_3.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/LevMar_minimized_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/LevMar_minimized_3.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_Iter_o_gamma_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_armijo_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_armijo_3.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_fixed_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_fixed_3.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_minimized_2.png
Dosyayı Görüntüle
BIN
Work2/scripts/figures/StDes_minimized_3.png
Dosyayı Görüntüle
+ 49
- 0
Work2/scripts/fmin_bisection.m
Dosyayı Görüntüle
| @@ -0,0 +1,49 @@ | |||
| function [a, b, k, n] = fmin_bisection(fun, alpha, beta, epsilon, lambda) | |||
| % Bisection method for finding the local minimum of a function. | |||
| % | |||
| % fun: The objective function | |||
| % alpha: (number) The starting point of the interval in which we seek | |||
| % for minimum | |||
| % beta: (number) The ending point of the interval in which we seek | |||
| % for minimum | |||
| % epsilon: (number) The epsilon value (distance from midpoint) | |||
| % lambda: (number) The lambda value (accuracy) | |||
| % | |||
| % return: | |||
| % a: (vector) Starting points of the interval for each iteration | |||
| % b: (vector) Ending points of the interval for each iteration | |||
| % k: (number) The number of iterations | |||
| % n: (number) The calls of objective function fun_expr | |||
| % | |||
| % Error checking | |||
| if alpha > beta || 2*epsilon >= lambda || lambda <= 0 | |||
| error ('Input criteria not met') | |||
| end | |||
| % Init | |||
| a = alpha; | |||
| b = beta; | |||
| n = 0; | |||
| k=1; | |||
| while b(k) - a(k) > lambda | |||
| % bisect [a,b] | |||
| mid = (a(k) + b(k)) / 2; | |||
| x_1 = mid - epsilon; | |||
| x_2 = mid + epsilon; | |||
| % set new search interval | |||
| k = k + 1; | |||
| if fun(x_1) < fun(x_2) | |||
| a(k) = a(k-1); | |||
| b(k) = x_2; | |||
| else | |||
| a(k) = x_1; | |||
| b(k) = b(k-1); | |||
| end | |||
| end | |||
| end | |||
+ 17
- 9
Work2/scripts/gamma_armijo.m
Dosyayı Görüntüle
| @@ -1,25 +1,33 @@ | |||
| function [gamma] = gamma_armijo(f, grad_f, x0) | |||
| function [gamma] = gamma_armijo(f, grad_f, dk, xk) | |||
| % Calculates the best step based on amijo method | |||
| % | |||
| % f(xk− γk*∇f(xk)) ≤ f(xk) − σ*γk*∥∇f(xk)∥^2 | |||
| % f(xk+ γk*dk) ≤ f(xk) + σ * γk * dk^T * ∇f(xk) | |||
| % γk = β*γk_0 | |||
| % | |||
| % f: Objective function | |||
| % x0: Initial (x,y) point | |||
| % grad_fun: Gradient function of f | |||
| % dk: Current value of selected direction -∇f or -inv{H}*∇f or -inv{H + lI}*∇f | |||
| % xk: Current point (x,y) | |||
| % beta: beta factor in (0, 1) | |||
| % signam: sigma factor in (0,1) | |||
| % beta: beta factor in [0.1, 0.5] | |||
| % signam: sigma factor in (0, 0.1] | |||
| global amijo_beta | |||
| global amijo_sigma | |||
| gf = grad_f(xk(1), xk(2)); | |||
| gamma = 1; % Start with a step size of 1 | |||
| grad = grad_f(x0(1), x0(2)); | |||
| % Perform Armijo line search | |||
| while f(x0(1) - gamma * grad(1), x0(2) - gamma * grad(2)) > ... | |||
| f(x0(1), x0(2)) - amijo_sigma * gamma * norm(grad)^2 | |||
| while f(xk(1) + gamma * dk(1), xk(2) + gamma * dk(2)) > ... | |||
| f(xk(1), xk(2)) + amijo_sigma * gamma * dk' * gf | |||
| %while f(xk(1) + gamma * dk(1), xk(2) + gamma * dk(2)) > ... | |||
| % f(xk(1), xk(2)) + amijo_sigma * gamma * norm(dk)^2 | |||
| gamma = amijo_beta * gamma; % Reduce step size | |||
| if gamma < 1e-12 % Safeguard to prevent infinite reduction | |||
| warning('Armijo step size became too small.'); | |||
| break; | |||
| end | |||
| end | |||
| end | |||
+ 1
- 1
Work2/scripts/gamma_fixed.m
Dosyayı Görüntüle
| @@ -1,4 +1,4 @@ | |||
| function [gamma] = gamma_fixed(~, ~, ~) | |||
| function [gamma] = gamma_fixed(~, ~, ~, ~) | |||
| % Return a fixed step | |||
| % | |||
| % This is for completion and code symmetry. | |||
+ 19
- 13
Work2/scripts/gamma_minimized.m
Dosyayı Görüntüle
| @@ -1,18 +1,24 @@ | |||
| function [gamma] = gamma_minimized(f, grad_f, x0) | |||
| % Calculates the step based on minimizing f(xk− γ*∇f(xk)) | |||
| function [gamma] = gamma_minimized(f, ~, dk, xk) | |||
| % Calculates the step based on minimizing f(xk− γk*dk) | |||
| % | |||
| % | |||
| % f: Objective function | |||
| % grad_f: Gradient of objective function | |||
| % x0: Initial (x,y) point | |||
| % f: Objective function | |||
| % ~: Gradient function of f - Not used | |||
| % dk: Current value of selected direction -∇f or -inv{H}*∇f or -inv{H + lI}*∇f | |||
| % xk: Current point (x,y) | |||
| % Define the line search function g(gamma) = f(x0 - gamma * grad) | |||
| grad = grad_f(x0(1), x0(2)); | |||
| g = @(gamma) f(x0(1) - gamma * grad(1), x0(2) - gamma * grad(2)); | |||
| % Define the line search function fmin(g) = f(xk - g * dk) | |||
| fmin = @(g) f(xk(1) + g*dk(1), xk(2) + g*dk(2)); | |||
| % Perform line search | |||
| gamma = fminbnd(g, 0, 1); | |||
| % ToDo: Check if we can use fmin_bisection_der | |||
| % from the previous assigment here! | |||
| % find g that minimizes fmin | |||
| e = 0.0001; | |||
| l = 0.001; | |||
| [a,b,k,~] = fmin_bisection(fmin, 0, 5, e, l); | |||
| gamma = 0.5*(a(k) + b(k)); | |||
| % Define the line search function fmin(g) = f(xk - g * dk) | |||
| %fmin = @(g) f(xk(1) - gamma * dk(1), xk(2) - gamma * dk(2)); | |||
| % find g that minimizes fmin | |||
| %gamma = fminbnd(g, 0, 1); | |||
| end | |||
+ 24
- 13
Work2/scripts/method_lev_mar.m
Dosyayı Görüntüle
| @@ -1,8 +1,9 @@ | |||
| function [x_vals, f_vals, k] = method_lev_mar(f, grad_f, hessian_f, m, x0, tol, max_iter, mode) | |||
| function [x_vals, f_vals, k] = method_lev_mar(f, grad_f, hessian_f, e, xk, tol, max_iter, mode) | |||
| % f: Objective function | |||
| % grad_f: Gradient of the function | |||
| % hessian_f: Hessian of the function | |||
| % x0: Initial point [x0, y0] | |||
| % e: mu offset for hessian damping H' = H_k + mI | |||
| % xk: Initial point [xk, yk] | |||
| % tol: Tolerance for stopping criterion | |||
| % max_iter: Maximum number of iterations | |||
| @@ -12,36 +13,46 @@ function [x_vals, f_vals, k] = method_lev_mar(f, grad_f, hessian_f, m, x0, tol, | |||
| if strcmp(mode, 'armijo') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_armijo(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_armijo(f, grad_f, dk, xk); | |||
| elseif strcmp(mode, 'minimized') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_minimized(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_minimized(f, grad_f, dk, xk); | |||
| else % mode == 'fixed' | |||
| gamma_f = @(f, grad_f, x0) gamma_fixed(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_fixed(f, grad_f, dk, xk); | |||
| end | |||
| x_vals = x0; % Store iterations | |||
| f_vals = f(x0(1), x0(2)); | |||
| x_vals = xk; % Store iterations | |||
| f_vals = f(xk(1), xk(2)); | |||
| for k = 1:max_iter | |||
| grad = grad_f(x0(1), x0(2)); | |||
| grad = grad_f(xk(1), xk(2)); | |||
| % Check for convergence | |||
| if norm(grad) < tol | |||
| break; | |||
| end | |||
| hess = hessian_f(x0(1), x0(2)); | |||
| mI = m * eye(size(hess)); | |||
| hess = hessian_f(xk(1), xk(2)); | |||
| % Check if hessian is not positive defined | |||
| lmin = min(eig(hess)); | |||
| if lmin <= 0 | |||
| m = abs(lmin) + e; | |||
| mI = m * eye(size(hess)); | |||
| nev = eig(hess + mI); | |||
| if min(nev) <= 0 | |||
| warning('Can not normalize hessian matrix.'); | |||
| end | |||
| end | |||
| % Solve for search direction using Newton's step | |||
| dk = - inv(hess + mI) * grad; | |||
| % Calculate gamma | |||
| gamma = gamma_f(f, grad_f, x0); | |||
| gk = gamma_f(f, grad_f, dk, xk); | |||
| x_next = x0 + gamma * dk'; % Update step | |||
| x_next = xk + gk * dk'; % Update step | |||
| f_next = f(x_next(1), x_next(2)); | |||
| x0 = x_next; % Update point | |||
| xk = x_next; % Update point | |||
| x_vals = [x_vals; x_next]; % Store values | |||
| f_vals = [f_vals; f_next]; % Store function values | |||
| end | |||
+ 11
- 11
Work2/scripts/method_newton.m
Dosyayı Görüntüle
| @@ -1,4 +1,4 @@ | |||
| function [x_vals, f_vals, k] = method_newton(f, grad_f, hessian_f, x0, tol, max_iter, mode) | |||
| function [x_vals, f_vals, k] = method_newton(f, grad_f, hessian_f, xk, tol, max_iter, mode) | |||
| % f: Objective function | |||
| % grad_f: Gradient of the function | |||
| % hessian_f: Hessian of the function | |||
| @@ -12,35 +12,35 @@ function [x_vals, f_vals, k] = method_newton(f, grad_f, hessian_f, x0, tol, max_ | |||
| if strcmp(mode, 'armijo') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_armijo(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_armijo(f, grad_f, dk, xk); | |||
| elseif strcmp(mode, 'minimized') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_minimized(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_minimized(f, grad_f, dk, xk); | |||
| else % mode == 'fixed' | |||
| gamma_f = @(f, grad_f, x0) gamma_fixed(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_fixed(f, grad_f, dk, xk); | |||
| end | |||
| x_vals = x0; % Store iterations | |||
| f_vals = f(x0(1), x0(2)); | |||
| x_vals = xk; % Store iterations | |||
| f_vals = f(xk(1), xk(2)); | |||
| for k = 1:max_iter | |||
| grad = grad_f(x0(1), x0(2)); | |||
| grad = grad_f(xk(1), xk(2)); | |||
| % Check for convergence | |||
| if norm(grad) < tol | |||
| break; | |||
| end | |||
| hess = hessian_f(x0(1), x0(2)); | |||
| hess = hessian_f(xk(1), xk(2)); | |||
| % Solve for search direction using Newton's step | |||
| dk = - inv(hess) * grad; | |||
| % Calculate gamma | |||
| gamma = gamma_f(f, grad_f, x0); | |||
| gk = gamma_f(f, grad_f, dk, xk); | |||
| x_next = x0 + gamma * dk'; % Update step | |||
| x_next = xk + gk * dk'; % Update step | |||
| f_next = f(x_next(1), x_next(2)); | |||
| x0 = x_next; % Update point | |||
| xk = x_next; % Update point | |||
| x_vals = [x_vals; x_next]; % Store values | |||
| f_vals = [f_vals; f_next]; % Store function values | |||
| end | |||
+ 11
- 11
Work2/scripts/method_steepest_descent.m
Dosyayı Görüntüle
| @@ -1,7 +1,7 @@ | |||
| function [x_vals, f_vals, k] = method_steepest_descent(f, grad_f, x0, tol, max_iter, mode) | |||
| function [x_vals, f_vals, k] = method_steepest_descent(f, grad_f, xk, tol, max_iter, mode) | |||
| % f: Objective function | |||
| % grad_f: Gradient of the function | |||
| % x0: Initial point [x0, y0] | |||
| % xk: Initial point [x0, y0] | |||
| % tol: Tolerance for stopping criterion | |||
| % max_iter: Maximum number of iterations | |||
| @@ -10,19 +10,19 @@ function [x_vals, f_vals, k] = method_steepest_descent(f, grad_f, x0, tol, max_i | |||
| % k: Number of iterations | |||
| if strcmp(mode, 'armijo') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_armijo(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_armijo(f, grad_f, dk, xk); | |||
| elseif strcmp(mode, 'minimized') == 1 | |||
| gamma_f = @(f, grad_f, x0) gamma_minimized(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_minimized(f, grad_f, dk, xk); | |||
| else % mode == 'fixed' | |||
| gamma_f = @(f, grad_f, x0) gamma_fixed(f, grad_f, x0); | |||
| gamma_f = @(f, grad_f, dk, xk) gamma_fixed(f, grad_f, dk, xk); | |||
| end | |||
| % Storage for iterations, begin with the first point | |||
| x_vals = x0; | |||
| f_vals = f(x0(1), x0(2)); | |||
| x_vals = xk; | |||
| f_vals = f(xk(1), xk(2)); | |||
| for k = 1:max_iter | |||
| grad = grad_f(x0(1), x0(2)); | |||
| grad = grad_f(xk(1), xk(2)); | |||
| % Check for convergence | |||
| if norm(grad) < tol | |||
| @@ -31,12 +31,12 @@ function [x_vals, f_vals, k] = method_steepest_descent(f, grad_f, x0, tol, max_i | |||
| dk = - grad; | |||
| % Calculate gamma | |||
| gk = gamma_f(f, grad_f, x0); | |||
| gk = gamma_f(f, grad_f, dk, xk); | |||
| x_next = x0 + gk * dk'; % Update step | |||
| x_next = xk + gk * dk'; % Update step | |||
| f_next = f(x_next(1), x_next(2)); | |||
| x0 = x_next; % Update point | |||
| xk = x_next; % Update point | |||
| x_vals = [x_vals; x_next]; % Store values | |||
| f_vals = [f_vals; f_next]; % Store function values | |||
| end | |||
+ 1
- 1
Work2/scripts/plotPointsOverContour.m
Dosyayı Görüntüle
| @@ -21,7 +21,7 @@ function plotPointsOverContour(points, contour_fun, x_lim, y_lim, size, plot_tit | |||
| Z = contour_fun(X, Y); | |||
| % 2D plot | |||
| figure('Name', '(x,y)', 'NumberTitle', 'off'); | |||
| figure('Name', '(x,y) convergence', 'NumberTitle', 'off'); | |||
| set(gcf, 'Position', [100, 100, image_width, image_height]); % Set the figure size | |||
| plot(points(:, 1), points(:, 2), '-or'); | |||
| hold on | |||