17 arquivos alterados com 335 adições e 98 exclusões
Visão dividida
Opções de diferenças
-
BINProject/report/Project_report.pdf
-
+313 -0Project/report/Project_report.tex
-
BINProject/report/report.pdf
-
+0 -90Project/report/report.tex
-
BINProject/scripts/figures/constV_pop_100mut_0.005.png
-
BINProject/scripts/figures/constV_pop_100mut_0.01.png
-
BINProject/scripts/figures/constV_pop_26mut_0.005.png
-
BINProject/scripts/figures/constV_pop_26mut_0.01.png
-
BINProject/scripts/figures/constV_pop_36mut_0.1.png
-
BINProject/scripts/figures/constV_pop_50mut_0.002.png
-
BINProject/scripts/figures/constV_pop_50mut_0.005.png
-
BINProject/scripts/figures/constV_pop_50mut_0.01.png
-
BINProject/scripts/figures/constV_pop_50mut_0.02.png
-
BINProject/scripts/figures/constV_pop_50mut_0.05.png
-
BINProject/scripts/figures/constV_pop_76mut_0.005.png
-
BINProject/scripts/figures/constV_pop_76mut_0.01.png
-
+22 -8Project/scripts/minimizeConstV.m
BIN
Project/report/Project_report.pdf
Ver arquivo
+ 313
- 0
Project/report/Project_report.tex
Ver arquivo
| @@ -0,0 +1,313 @@ | |||
| % !TEX TS-program = xelatex | |||
| % !TEX encoding = UTF-8 Unicode | |||
| % !TEX spellcheck = el-GR | |||
| % | |||
| % Optimization techniques project report | |||
| % | |||
| % Requires compilation with pdfLaTeX or XeLaTeX | |||
| % | |||
| % authors: | |||
| % Χρήστος Χουτουρίδης ΑΕΜ 8997 | |||
| % cchoutou@ece.auth.gr | |||
| % | |||
| % Options: | |||
| % | |||
| % 1) mainlang=<language> | |||
| % Default: english | |||
| % Set the default language of the document which affects hyphenations, | |||
| % localization (section, dates, etc...) | |||
| % | |||
| % example: \documentclass[mainlang=greek]{AUThReport} | |||
| % | |||
| % 2) <language> | |||
| % Add hyphenation and typesetting support for other languages | |||
| % Currently supports: english, greek, german, frenc | |||
| % | |||
| % example: \documentclass[english, greek]{AUThReport} | |||
| % | |||
| % 3) short: Requests a shorter title for the document | |||
| % Default: no short | |||
| % | |||
| % example: \documentclass[short]{AUThReport} | |||
| % | |||
| \documentclass[a4paper, 11pt, mainlang=greek, english]{AUThReport} | |||
| \CurrentDate{\today} | |||
| % Document setup | |||
| %--------------------------------- | |||
| % \WorkGroup{Ομάδα Χ} | |||
| \AuthorName{Χρήστος Χουτουρίδης} | |||
| \AuthorMail{cchoutou@ece.auth.gr} | |||
| \AuthorAEM{8997} | |||
| %\CoAuthorName{Όνομα Επίθετο} | |||
| %\CoAuthorAEM{AEM} | |||
| %\CoAuthorMail{xxx@ece.auth.gr} | |||
| \DocTitle{Project: Γενετικοί αλγόριθμοι} | |||
| \DocSubTitle{Ελαχιστοποίηση συνάρτησης πολλών μεταβλητών} | |||
| \Department{Τμήμα ΗΜΜΥ. Τομέας Ηλεκτρονικής} | |||
| \ClassName{Τεχνικές Βελτιστοποίησης} | |||
| % | |||
| \InstructorName{Γ. Ροβιθάκης} | |||
| \InstructorMail{rovithak@auth.gr} | |||
| \CoInstructorName{Θ. Αφορόζη} | |||
| \CoInstructorMail{taforozi@ece.auth.gr} | |||
| % Local package requirements | |||
| %--------------------------------- | |||
| \usepackage{enumitem} | |||
| \usepackage{tabularx} | |||
| \usepackage{array} | |||
| \usepackage{multirow} | |||
| \usepackage{float} | |||
| \usepackage{xcolor} | |||
| \usepackage{soul} | |||
| \usepackage{amsmath} | |||
| \usepackage{footnote} | |||
| \usepackage{footmisc} | |||
| \usepackage[labelformat=empty]{subcaption} | |||
| \begin{document} | |||
| \InsertTitle | |||
| %\tableofcontents | |||
| \section{Εισαγωγή} | |||
| Η παρούσα εργασία αφορά την ελαχιστοποίηση συνάρτησης πολλών μεταβλητών, χρησιμοποιώντας \textbf{γενετικό αλγόριθμο}. | |||
| Στην παρούσα εργασία προσπαθήσαμε να βελτιστοποιήσουμε το συνολικό χρόνο διέλευσης από ένα οδικό δίκτυο, το οποίο καλείται να εξυπηρετήσει ένα προκαθορισμένο όγκο οχημάτων ανά λεπτό, ενώ οι οδεύσεις του έχουν πεπερασμένη και προκαθορισμένη χωρητικότητα. | |||
| Η προσέγγιση του προβλήματος έγινε βάση δοθέντος από την εκφώνηση μαθηματικού μοντέλου για το χρόνο διέλευσης της κάθε κυκλοφοριακής κατεύθυνσης, το οποίο χρησιμοποιήθηκε ως συνάρτηση αξιολόγησης για το γενετικό αλγόριθμο που τον ελαχιστοποιεί. | |||
| \subsection{Παραδοτέα} | |||
| Τα παραδοτέα της εργασίας αποτελούνται από: | |||
| \begin{itemize} | |||
| \item Την παρούσα αναφορά. | |||
| \item Τον κατάλογο \textbf{scripts/}, που περιέχει τον κώδικα της MATLAB. | |||
| \item Το \href{https://git.hoo2.net/hoo2/OptimizationTechniques/src/branch/master/Project}{σύνδεσμο} με το αποθετήριο που περιέχει όλο το project με τον κώδικα της MATLAB, της αναφοράς και τα παραδοτέα. | |||
| \end{itemize} | |||
| \section{Γενετικοί Αλγόριθμοι} | |||
| Οι γενετικοί αλγόριθμοι (Genetic Algorithms - GAs) είναι αλγόριθμοι βελτιστοποίησης εμπνευσμένοι από τις αρχές της \textbf{φυσικής επιλογής} και της \textbf{γενετικής εξέλιξης}. | |||
| Σε αντίθεση με μεθόδους που χρησιμοποιούν παραγώγους, όπως αυτή της μέγιστης καθόδους, του Newtown κλπ, οι γενετικοί αλγόριθμοι αποτελούν τεχνικές ολικής βελτιστοποίησης, δηλαδή της εύρεσης του ολικού ελάχιστου μια συνάρτησης. | |||
| \par | |||
| Oι γενετικοί αλγόριθμοι λειτουργούν με τη δημιουργία ενός πληθυσμού πιθανών λύσεων, όπου κάθε λύση αναπαριστάται ως ένα χρωμόσωμα (διάνυσμα παραμέτρων). | |||
| Ο πληθυσμός εξελίσσεται μέσα από επαναλαμβανόμενες γενιές, εφαρμόζοντας τις εξής διαδικασίες: | |||
| \begin{itemize} | |||
| \item \textbf{Υπολογισμός καταλληλότητας (fitness evaluation)}: Κάθε λύση αξιολογείται βάσει μιας συνάρτησης καταλληλότητας, η οποία ποσοτικοποιεί πόσο καλή είναι σε σχέση με το πρόβλημα. | |||
| \item \textbf{Επιλογή (selection)}: Επιλέγονται οι καλύτερες λύσεις από τον τρέχοντα πληθυσμό, οι οποίες έχουν υψηλότερη πιθανότητα να περάσουν στα επόμενα στάδια. | |||
| \item \textbf{Διασταύρωση (crossover)}: Δημιουργούνται νέες λύσεις μέσω συνδυασμού δύο γονικών λύσεων, αναμιγνύοντας τα χαρακτηριστικά τους. | |||
| \item \textbf{Μετάλλαξη (mutation)}: Σε ορισμένες λύσεις εφαρμόζονται μικρές, τυχαίες τροποποιήσεις ώστε να διατηρηθεί η ποικιλομορφία του πληθυσμού και να αποφευχθεί η παγίδευση σε τοπικά ελάχιστα. | |||
| \item \textbf{Αντικατάσταση (replacement)}: Ο νέος πληθυσμός που προκύπτει αντικαθιστά τον παλιό, συνεχίζοντας τη διαδικασία μέχρι να ικανοποιηθεί κάποιο κριτήριο σύγκλισης. | |||
| \end{itemize} | |||
| Η συνεχής επανάληψη αυτών των διαδικασιών επιτρέπει στον γενετικό αλγόριθμο να αναζητήσει και να προσεγγίσει την καλύτερη δυνατή λύση μέσα στον χώρο των πιθανών λύσεων. | |||
| Στις επόμενες παραγράφους θα περιγράψουμε την υλοποίηση αυτών των διαδικασιών για την παρούσα εργασία. | |||
| \section{Μαθηματική διατύπωση του προβλήματος} | |||
| Το πρόβλημα μοντελοποιείται ως εξής: | |||
| \subsection*{Μεταβλητές Απόφασης} | |||
| Ο ρυθμός διέλευσης οχημάτων $x$ σε κάθε δρόμο $i$ για τους $n$ δρόμους δίνεται ως: | |||
| \[ | |||
| x = [x_1, x_2, \dots, x_n] | |||
| \] | |||
| \subsection*{Χρόνος κίνησης σε κάθε δρόμο} | |||
| Ο χρόνος διάσχισης $T_i$ του δρόμου $i$ συναρτήσει του ρυθμού διέλευσης είναι: | |||
| \begin{equation} | |||
| T_i(x_i) = t_i + \frac{a_i x_i}{1 - \frac{x_i}{c_i}}, \quad 0 \leq x_i < c_i, \quad i=1,2,\dots,n | |||
| \label{eq:Ti} | |||
| \end{equation} | |||
| \subsection*{Συνολικός χρόνος κίνησης} | |||
| Ο συνολικός χρόνος $T_total$ του οδικού δικτύου είναι: | |||
| \begin{equation} | |||
| T_{total} = \sum_{i=1}^{n} T_i(x_i) | |||
| \label{eq:Ttotal} | |||
| \end{equation} | |||
| \subsection*{Στόχος} | |||
| Ελαχιστοποίηση του συνολικού χρόνου διάσχισης: | |||
| \begin{equation} | |||
| \min_{x} T_{total} = \min_{x} \sum_{i=1}^{n} T_i(x_i) = \min_{x} \sum_{i=1}^{n} \left( t_i + \frac{a_i x_i}{1 - \frac{x_i}{c_i}} \right) | |||
| \label{eq:problem} | |||
| \end{equation} | |||
| \par | |||
| Εδώ θα πρέπει να τονίσουμε πως κάναμε την υπόθεση ότι ο χρόνος \boldmath $T_i$ αφορά \textbf{όλα τα οχήματα} που κινούνται το δεδομένο στιγμιότυπο στο δρόμο $i$\unboldmath. | |||
| Η εκφώνηση της άσκησης δεν ξεκαθαρίζει αν ο χρόνος $T_i$ αφορά το κάθε μεμονωμένο όχημα ή όλα. | |||
| Σε περίπτωση πάντως που αφορά το κάθε όχημα ξεχωριστά τότε το άθροισμα θα έπρεπε να τροποποιηθεί σε: $ \sum_{i=1}^{n} T_i(x_i)\cdot x_i = \sum_{i=1}^{n} \left( t_i + \frac{a_i x_i}{1 - \frac{x_i}{c_i}}\right)\cdot x_i $, το οποίο όμως δεν αλλάζει τη συμπεριφορά και τα ευρήματα της εργασίας. | |||
| \subsection*{Περιορισμοί} | |||
| 1. Ισορροπία εισερχομένων και εξερχομένων ροών σε κάθε κόμβο $j$: | |||
| \[ | |||
| \sum_{i \in incoming(j)} x_i = \sum_{k \in outgoing(j)} x_k, \quad \forall j | |||
| \] | |||
| 2. Περιορισμός ροής: | |||
| \[ | |||
| 0 \leq x_i \leq c_i, \quad \forall i | |||
| \] | |||
| 3. Ο συνολικός ρυθμός εισόδου στο δίκτυο: | |||
| \[ | |||
| \sum_{i=1}^{n} x_i = V | |||
| \] | |||
| \section{Υλοποίηση} | |||
| Πριν περάσουμε στην παρουσίαση των αποτελεσμάτων, καλό θα ήταν να περιγράψουμε τις εξελικτικές διαδικασίες που χρησιμοποιήσαμε. | |||
| Πιο συγκεκριμένα στην παρούσα εργασία υλοποιήσαμε ένα βρόχο με σταθερό αριθμό γενεών. | |||
| Σε κάθε γενιά του βρόχου: | |||
| \begin{itemize} | |||
| \item Εκτελούμε τη \textbf{συνάρτηση καταλληλότητας} η οποία απλώς χρησιμοποιεί τη μαθηματική μοντελοποίηση που περιγράψαμε στις εξισώσεις \ref{eq:Ti}, \ref{eq:Ttotal} για να αξιολογήσει τη συνολική απόδοση του πληθυσμού. | |||
| Με αυτό τον τρόπο έχουμε τον χρόνο σε κάθε δρόμο αλλά και τον συνολικό χρόνο για κάθε ένα χρωμόσωμα ξεχωριστά. | |||
| \item Έπειτα εκτελούμε \textbf{διασταύρωση}. | |||
| Για το σκοπό αυτό ταξινομούμε τον πληθυσμό με βάση τη συνολική ικανότητα και διαλέγουμε τις μισές καλύτερες λύσεις (χρωμοσώματα). | |||
| Αυτά τα χρησιμοποιούμε ως γονείς. | |||
| Με τυχαίο τρόπο επιλέγουμε δύο -- δύο κάθε φορά και από αυτό το ζευγάρι δημιουργούμε δύο παιδιά. | |||
| Το κάθε παιδί δημιουργείται με τη μέθοδο της \textbf{διακριτής διασταύρωσης}. | |||
| Εδώ να πούμε πως το πόσο μεγάλο κομμάτι από τον κάθε γονέα θα περάσει στο κάθε παιδί το επιλέγουμε με τυχαίο τρόπο. | |||
| \item Έπειτα ολοκληρώνουμε τη διαδικασία αντικατάσταση, χρησιμοποιώντας τη \textbf{στρατηγική '+'}. | |||
| Δηλαδή κρατάμε τους γονείς και συμπληρώνουμε το 2ο μισό του πληθυσμού με τα παιδιά. | |||
| \item Τέλος εκτελούμε τη διαδικασία της μετάλλαξης. | |||
| Σε αυτή τη διαδικασία συμμετέχουν όλα τα χρωμοσώματα και είναι τυχαίο φαινόμενο. | |||
| Με βάση μιας προκαθορισμένης πιθανότητας επιλέγουμε χρωμοσώματα από όλο τον πληθυσμό και τους αλλάζουμε την τιμή μιας τυχαίας παραμέτρου (χρόνος διέλευσης από ένα δρόμο). | |||
| Η νέα τιμή επιλέγεται πάλι τυχαία. | |||
| \end{itemize} | |||
| \section{Εκτέλεση - Συμπεριφορά} | |||
| Για την εκτέλεση του αλγόριθμου κινηθήκαμε σε δύο κατευθύνσεις. | |||
| Από τη μία κρατήσαμε σταθερό τον πληθυσμό και παρατηρήσαμε τη σύγκλιση του αλγόριθμου για διαφορετικές πιθανότητες μεταλλάξεων και από την άλλη κρατήσαμε την πιθανότητα σταθερή και δοκιμάσαμε διαφορετικό αριθμό χρωμοσωμάτων. | |||
| \subsection{Σταθερός αριθμός χρωμοσωμάτων} | |||
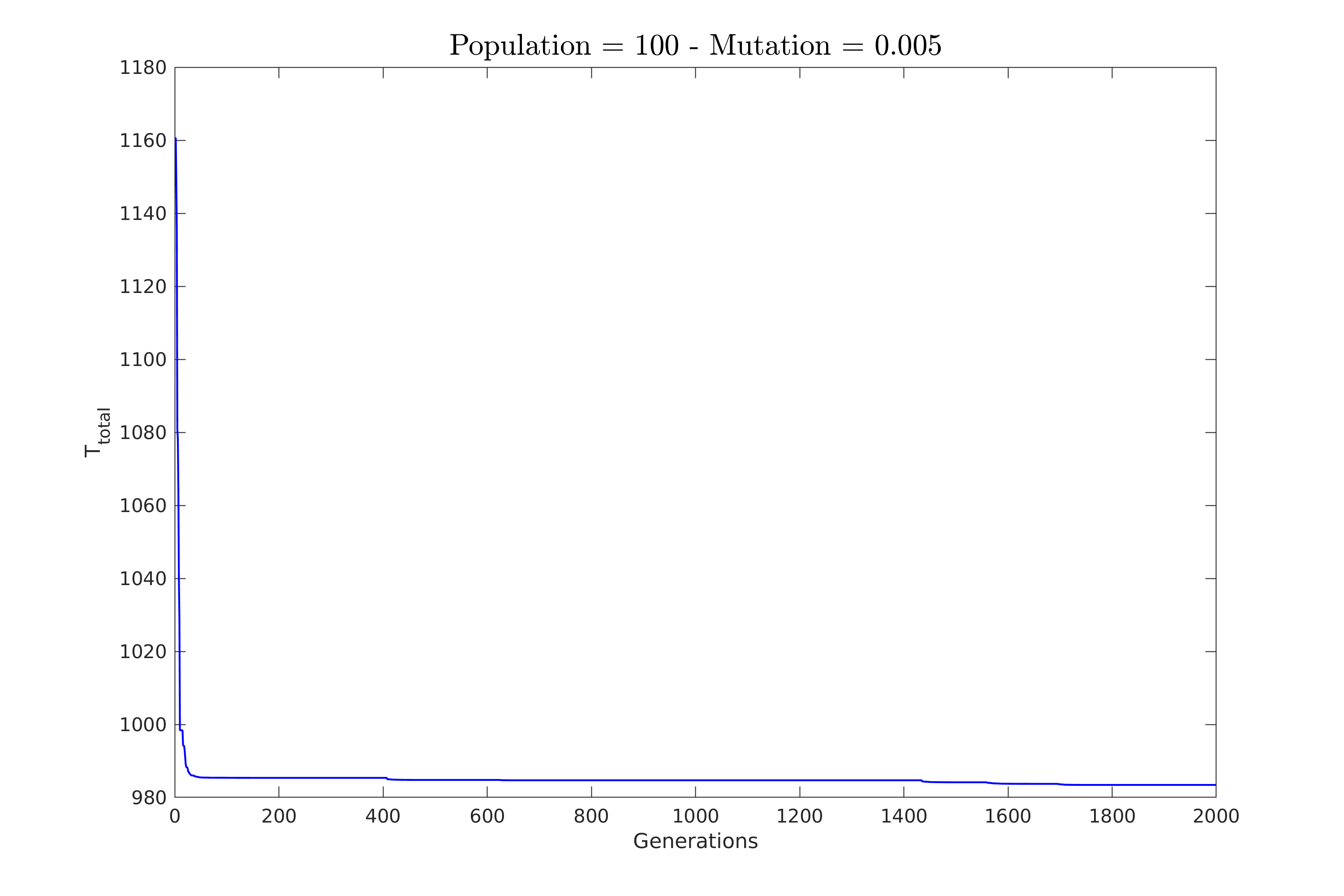
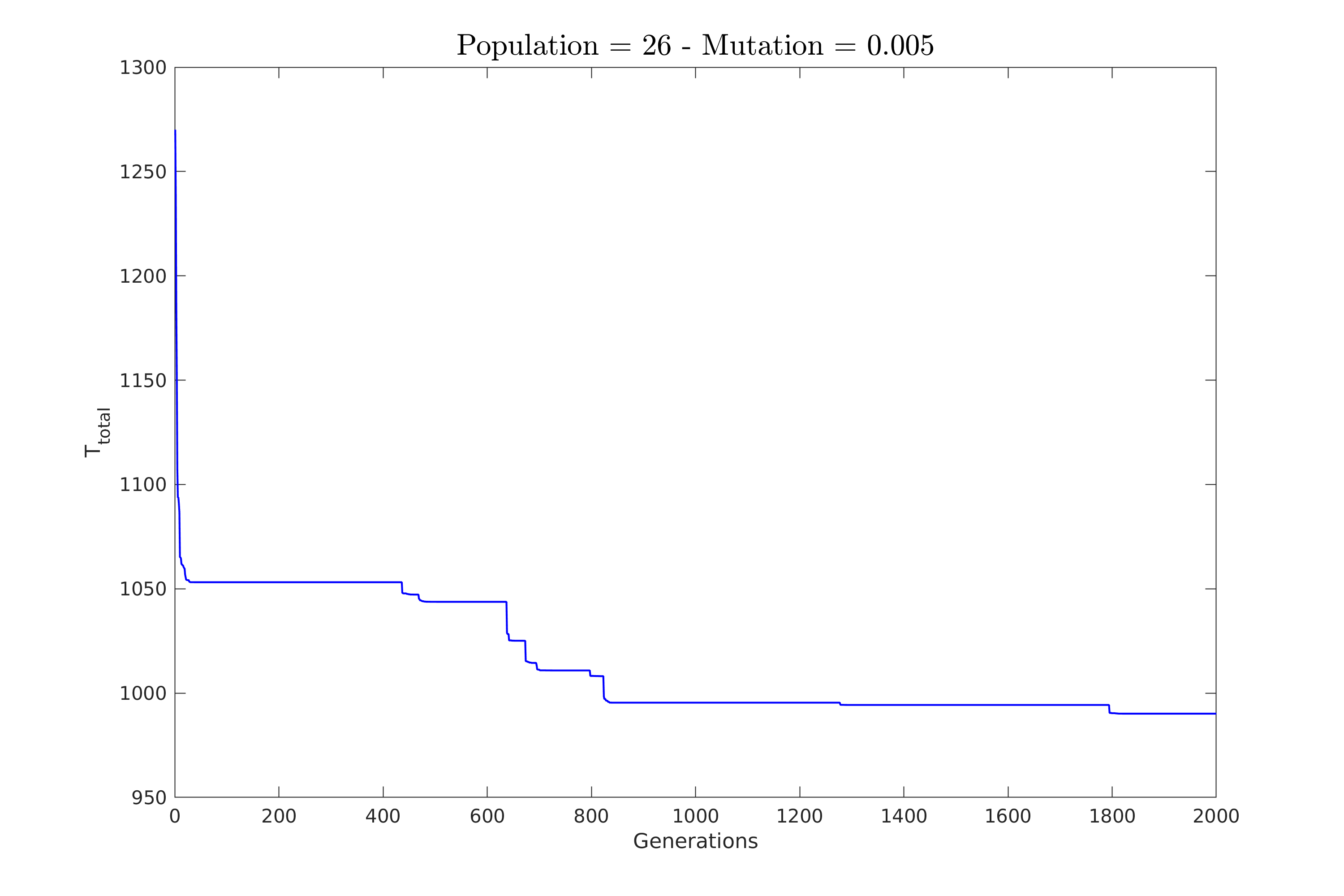
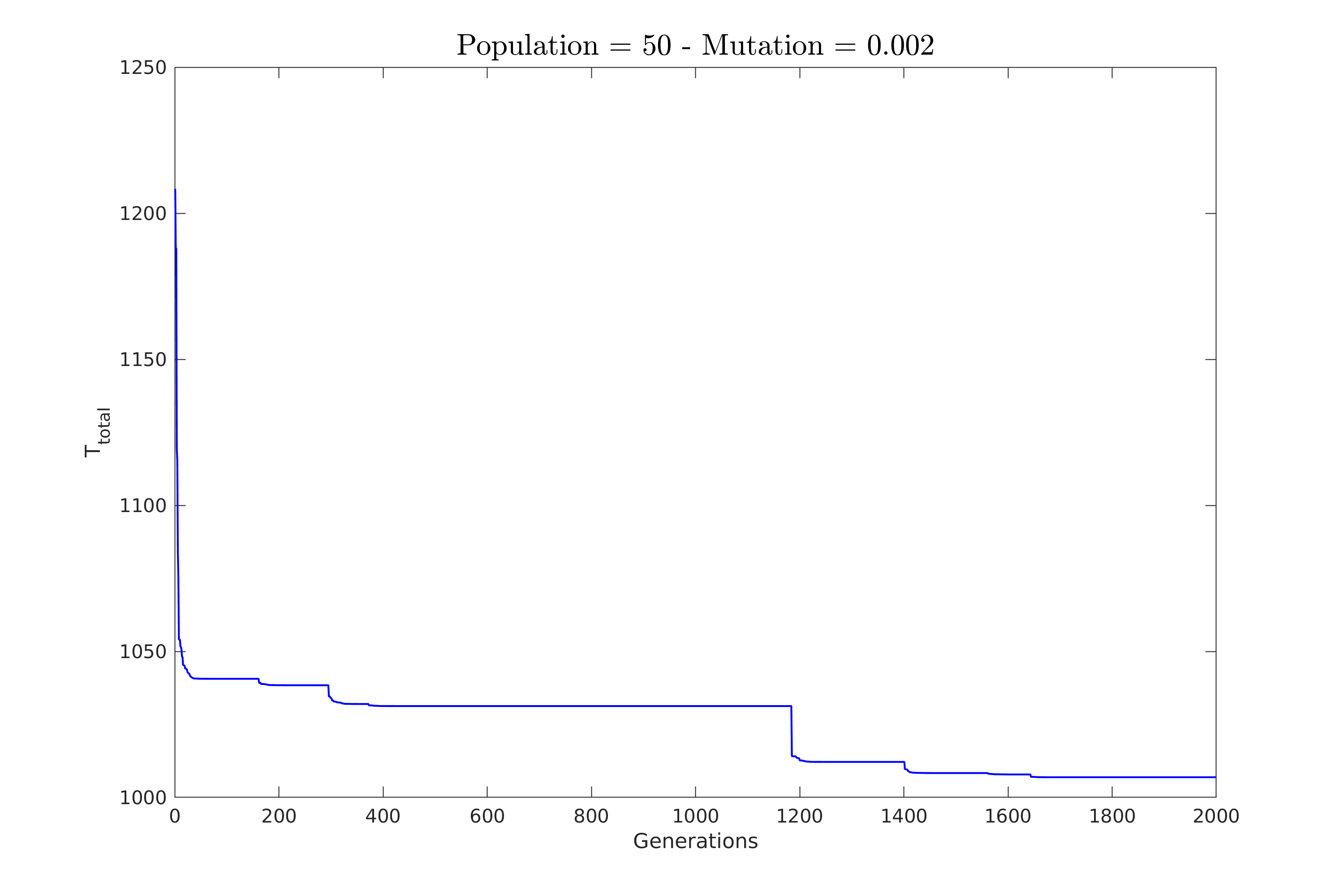
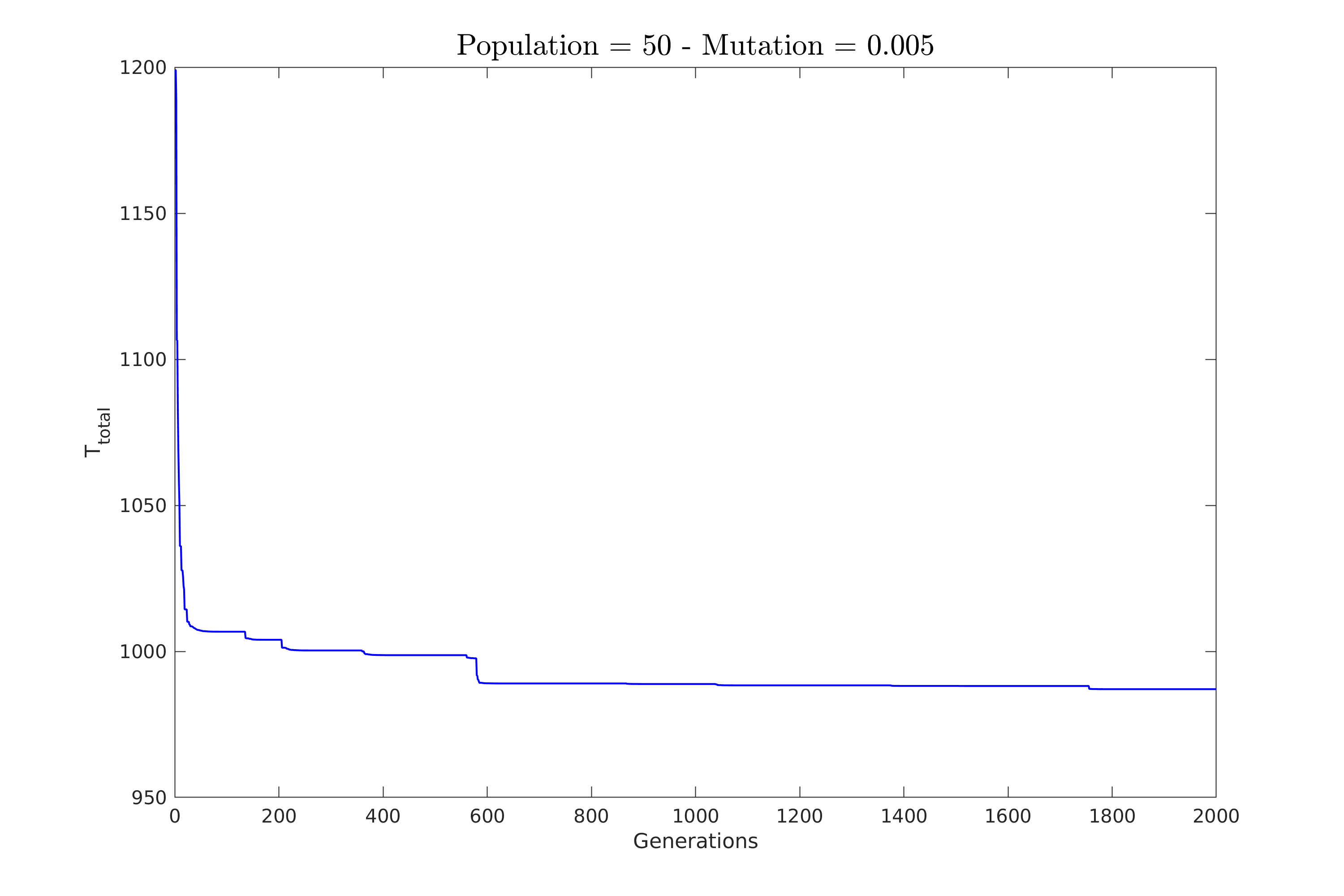
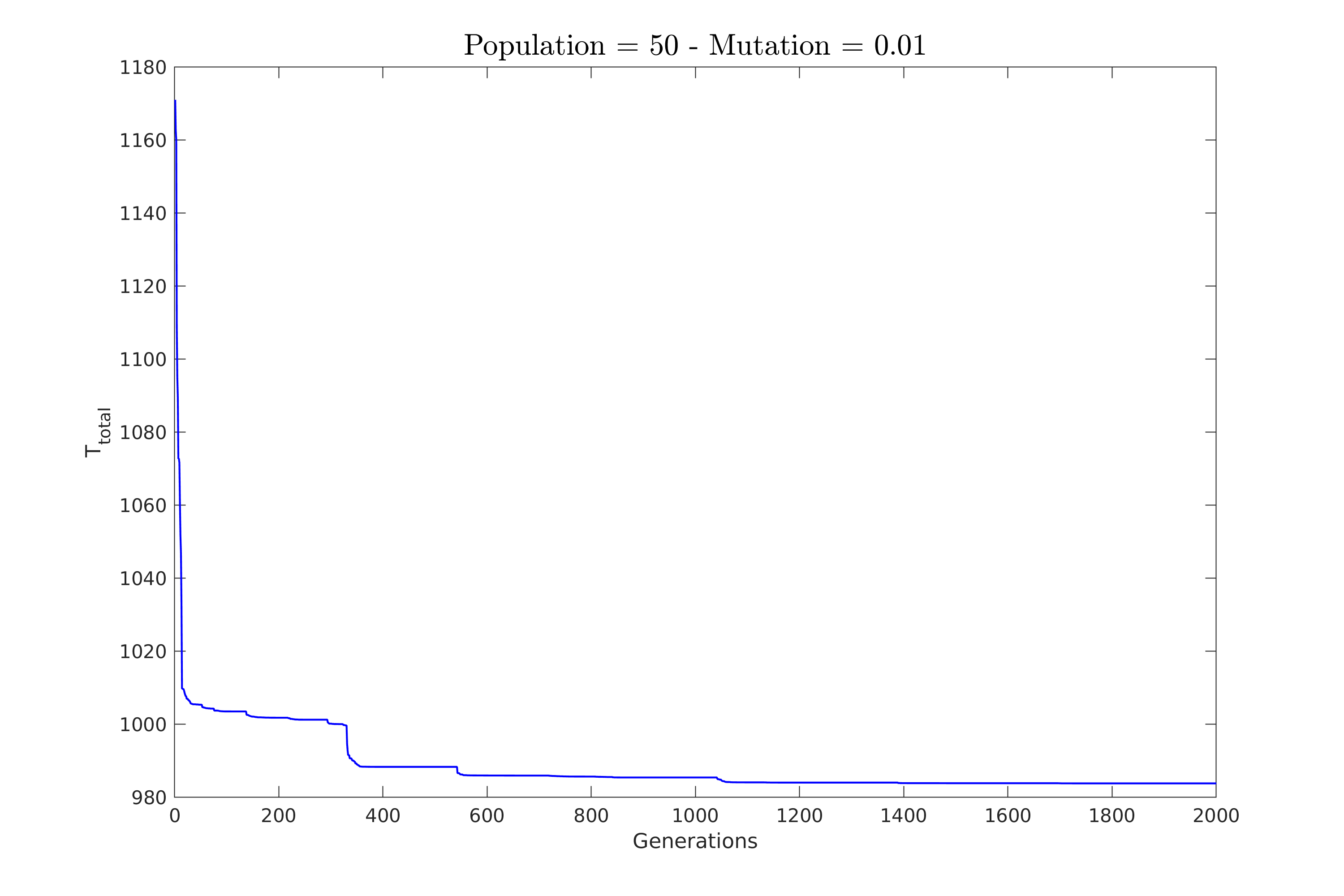
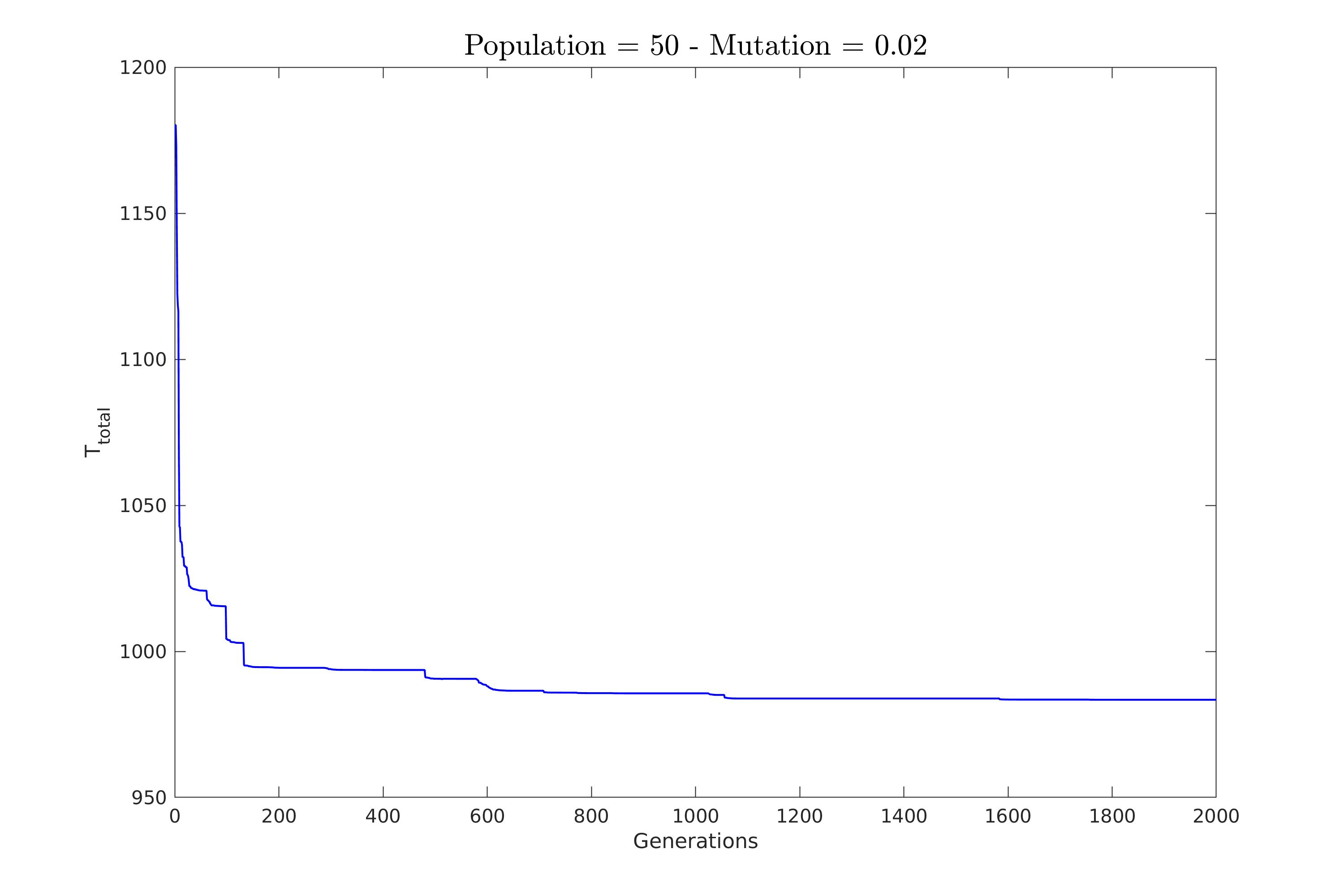
| Παρακάτω στο σχήμα \ref{fig:constV_pop_50} φαίνεται η πορεία σύγκλισης για την πρώτη περίπτωση. | |||
| Εδώ κρατήσαμε τον πληθυσμό στο 50 και δοκιμάσαμε πιθανότητες $0.2\%, 0.5\%, 1\%$ και $2\%$. | |||
| \textbf{Επιλέξαμε αρκετά μικρές τιμές για πιθανότητες ώστε να φανεί καλύτερα η συμπεριφορά του αλγόριθμου}. | |||
| Παρατηρούμε πως για μικρή πιθανότητα ο αλγόριθμος χρειάζεται πολλές γενεές για να συγκλίνει. | |||
| Επίσης, δείχνει να κολλάει σε κάποια υπο-βέλτιστη λύση για αρκετές γενεές. | |||
| Και τα δύο αυτά χαρακτηριστικά βέβαια ελαττώνονται με την αύξηση της πιθανότητας. | |||
| \par | |||
| Να σημειώσουμε εδώ ότι η αύξηση της πιθανότητας μετάλλαξης \textbf{αυξάνει ελάχιστα} τη υπολογιστική πολυπλοκότητα του αλγόριθμου. | |||
| \begin{figure}[H] | |||
| \centering | |||
| % First row | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.002.png} | |||
| \caption{Πιθανότητα: $0.2\%$} | |||
| \end{subfigure} | |||
| \hfill | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.005.png} | |||
| \caption{Πιθανότητα: $0.5\%$} | |||
| \end{subfigure} | |||
| % Second row | |||
| \vspace{1em} | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering¨ | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.01.png} | |||
| \caption{Πιθανότητα: $1\%$} | |||
| \end{subfigure} | |||
| \hfill | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.02.png} | |||
| \caption{Πιθανότητα: $2\%$} | |||
| \end{subfigure} | |||
| \caption{Σύγκριση της μεθόδου για σταθερό πληθυσμό $50$.} | |||
| \label{fig:constV_pop_50} | |||
| \end{figure} | |||
| \subsection{Σταθερή πιθανότητα μετάλλαξης} | |||
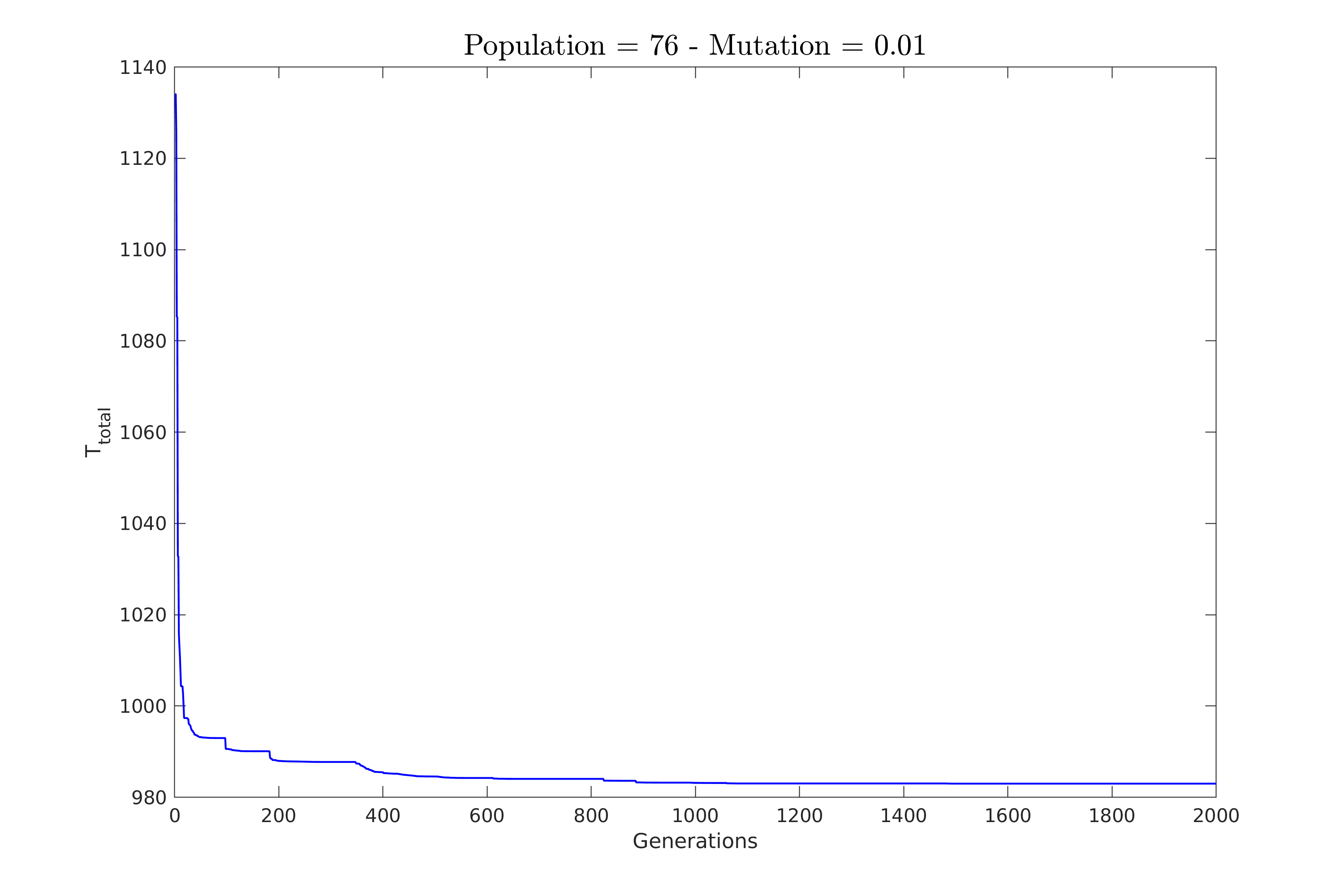
| Παρακάτω στο σχήμα \ref{fig:constV_mut_0.01} φαίνεται η πορεία σύγκλισης για την πρώτη περίπτωση. | |||
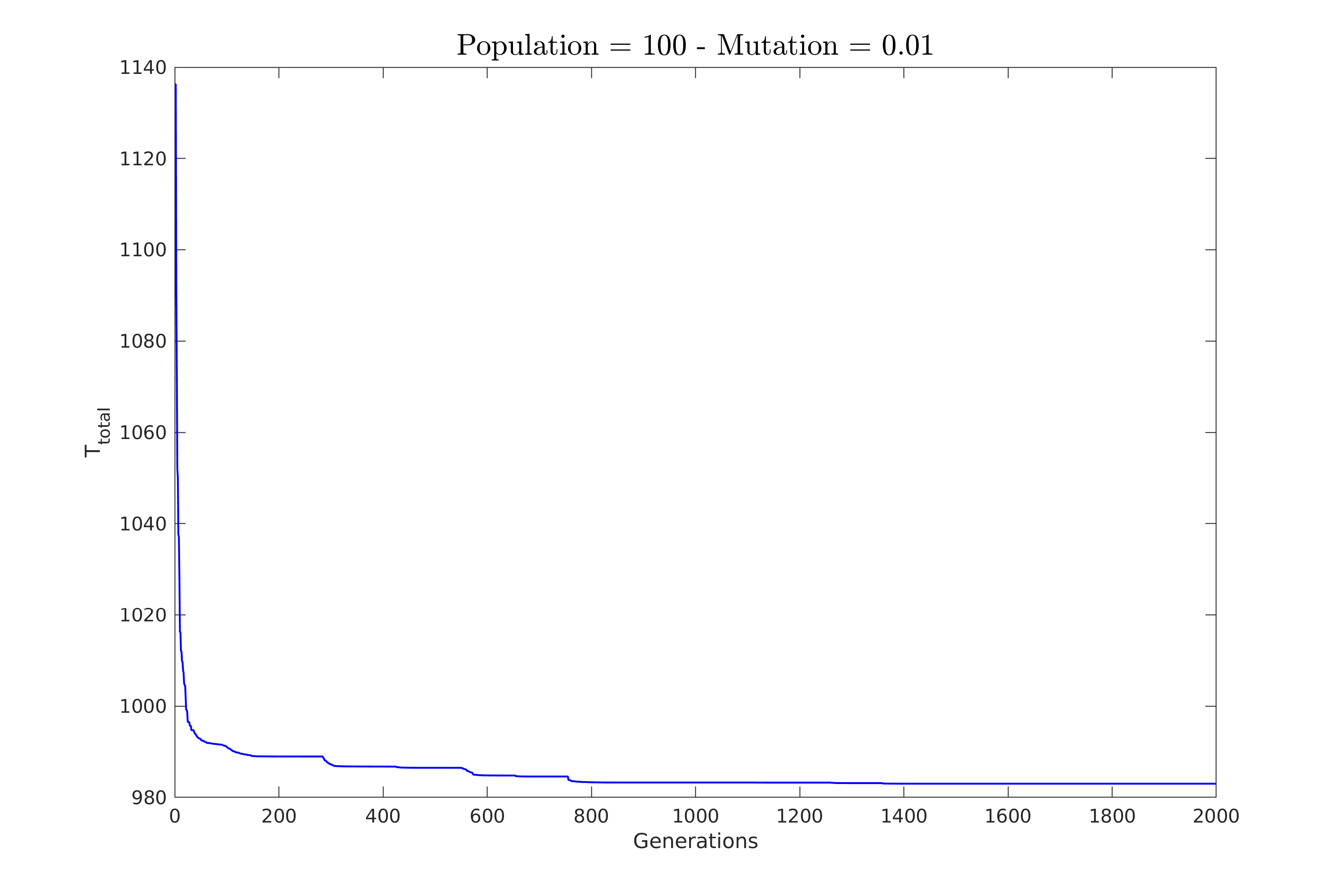
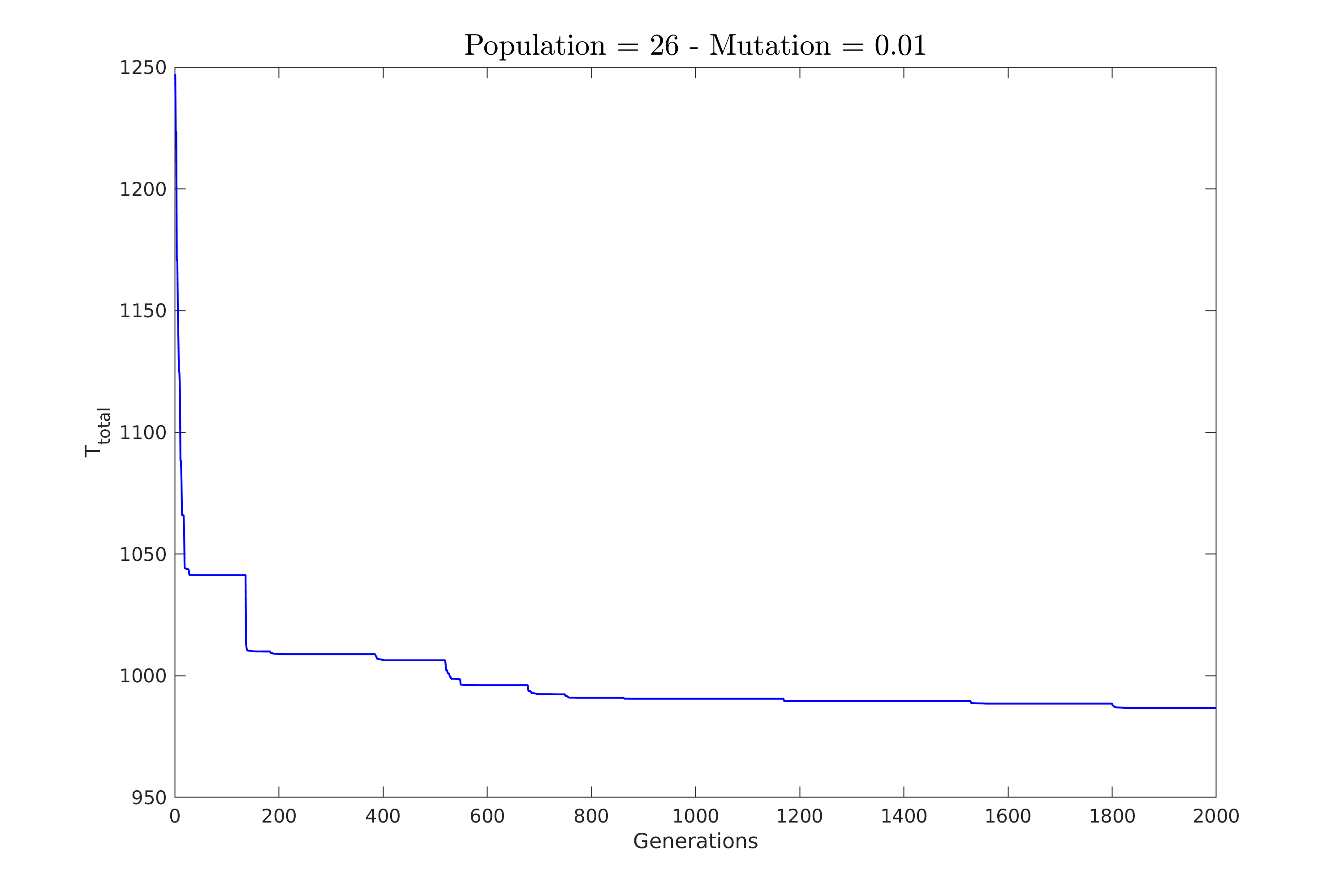
| Εδώ κρατήσαμε την πιθανότητα στο $1\%$ και δοκιμάσαμε πληθυσμούς των $26, 50, 76$ και $100$ χρωμοσωμάτων. | |||
| \textbf{Επιλέξαμε πάλι αρκετά μικρές τιμές για τον πληθυσμό ώστε να φανεί καλύτερα η συμπεριφορά του αλγόριθμου}. | |||
| Ομοίως παρατηρούμε πως μικροί πληθυσμοί χρειάζονται πολλές γενεές για να συγκλίνουν και οι μεταλλάξεις παρουσιάζουν απότομες μεταβολές. | |||
| Μεγαλύτεροι πληθυσμοί όμως φαίνεται ότι βοηθούν αρκετά στην συνολική πιθανότητα μετάλλαξης προς τη βέλτιστη λύση. | |||
| \begin{figure}[H] | |||
| \centering | |||
| % First row | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_26mut_0.01.png} | |||
| \caption{Πληθυσμός: $26$} | |||
| \end{subfigure} | |||
| \hfill | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.01.png} | |||
| \caption{Πληθυσμός: $50$} | |||
| \end{subfigure} | |||
| % Second row | |||
| \vspace{1em} | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_76mut_0.01.png} | |||
| \caption{Πληθυσμός: $76$} | |||
| \end{subfigure} | |||
| \hfill | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_100mut_0.01.png} | |||
| \caption{Πληθυσμός: $100$} | |||
| \end{subfigure} | |||
| \caption{Σύγκριση της μεθόδου για σταθερή πιθανότητα μετάλλαξης $1\%$.} | |||
| \label{fig:constV_mut_0.01} | |||
| \end{figure} | |||
| \par | |||
| Να σημειώσουμε εδώ ότι η αύξηση του πληθυσμού \textbf{αυξάνει σημαντικά} τη υπολογιστική πολυπλοκότητα του αλγόριθμου. | |||
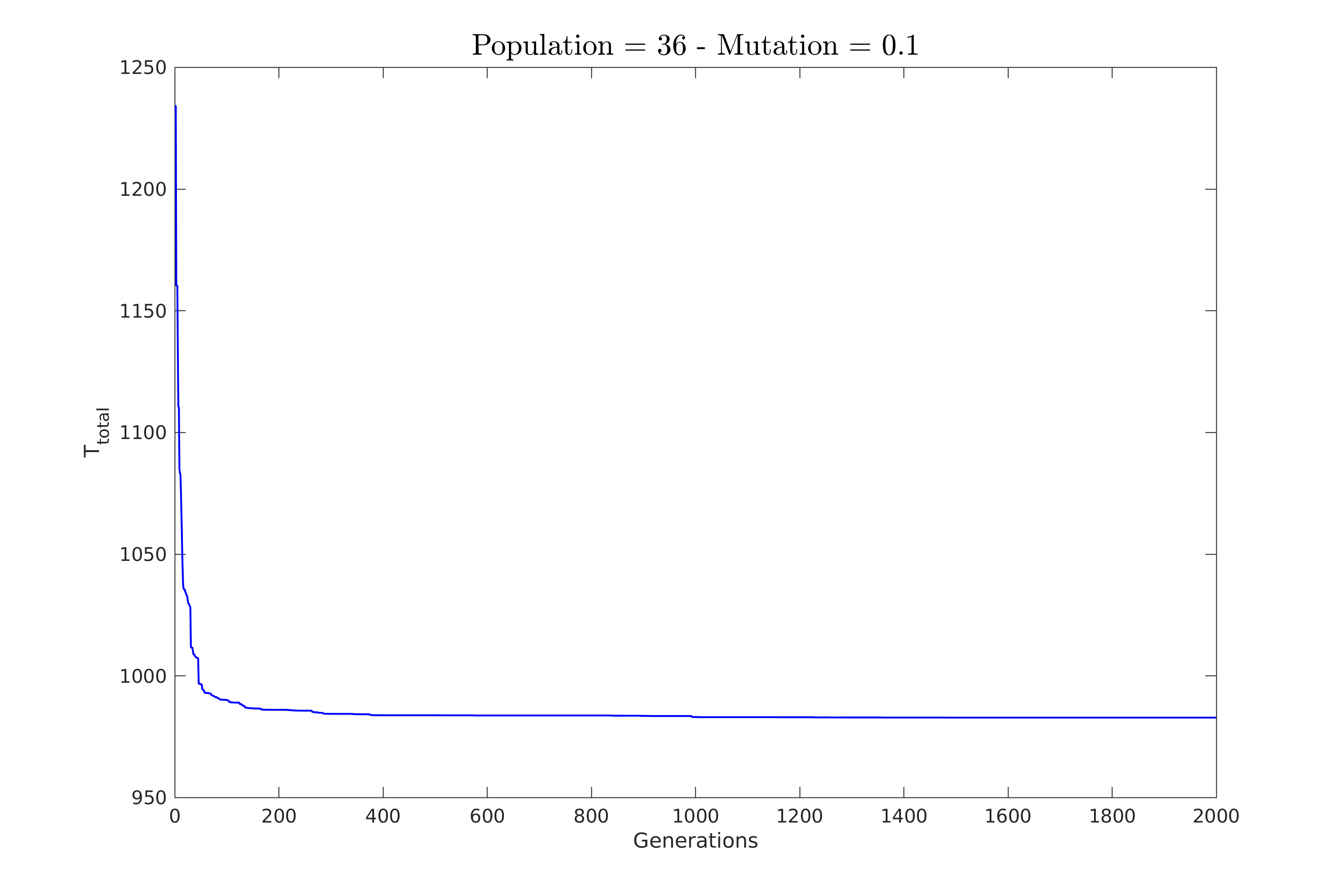
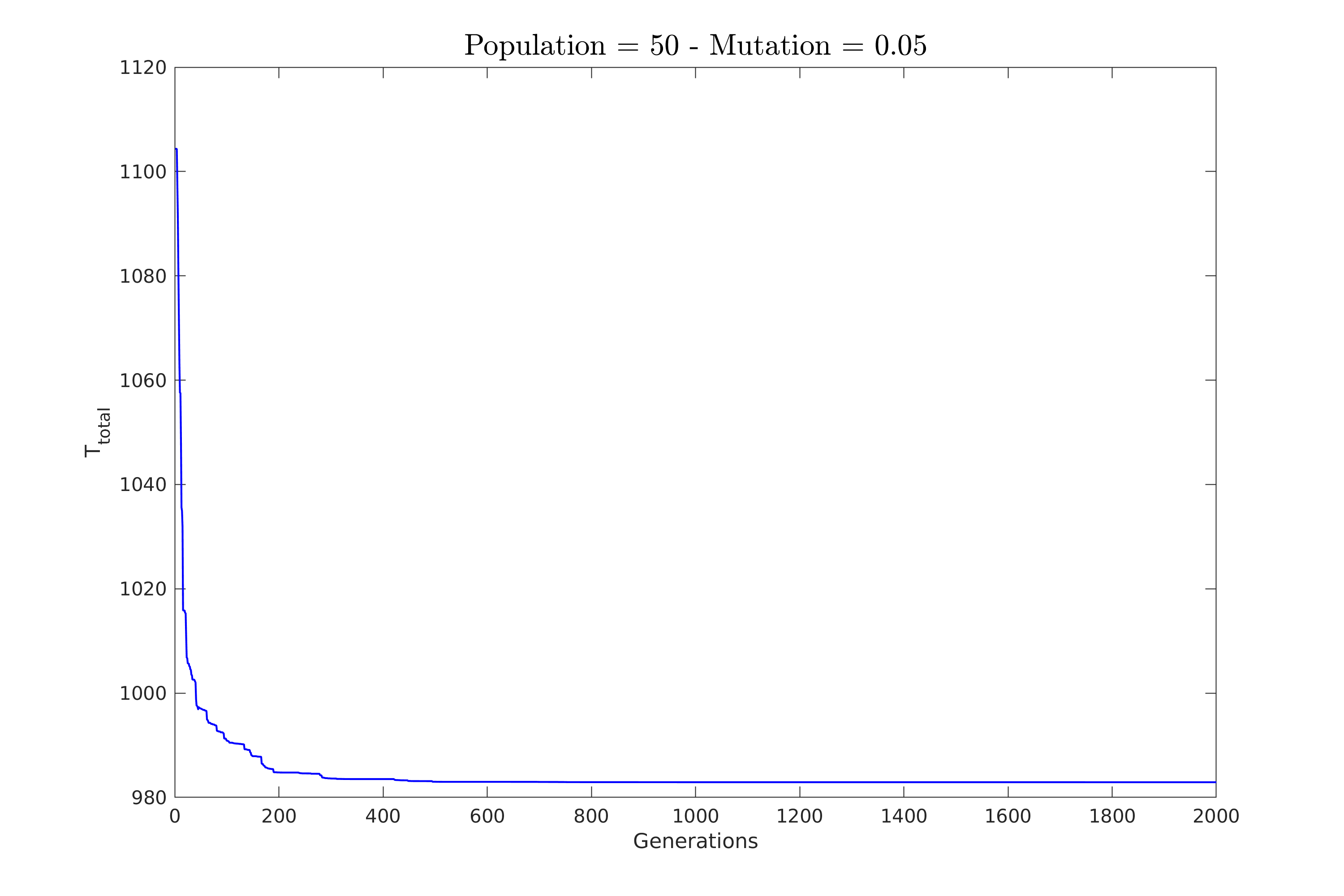
| Για αυτό το λόγο, όπως φαίνεται και στο παρακάτω σχήμα \ref{fig:constV_high_mut}, είναι προτιμότερο να επιλέξουμε \textbf{μεγάλη πιθανότητα μετάλλαξης με σχετικά μικρό πληθυσμό}. | |||
| Όπου βλέπουμε πως ο αλγόριθμος συμπεριφέρεται αρκετά καλά ακόμα και με μικρό πληθυσμό. | |||
| Αυτό θα μας δώσει γρήγορη σύγκλιση με σημαντικά μικρότερη υπολογιστική πολυπλοκότητα. | |||
| \begin{figure}[H] | |||
| \centering | |||
| % First row | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_50mut_0.05.png} | |||
| \caption{Πληθυσμός: $50$, Πιθανότητα: $5\%$} | |||
| \end{subfigure} | |||
| \hfill | |||
| \begin{subfigure}{0.45\textwidth} | |||
| \centering | |||
| \includegraphics[width=\linewidth]{../scripts/figures/constV_pop_36mut_0.1.png} | |||
| \caption{Πληθυσμός: $36$, Πιθανότητα: $10\%$} | |||
| \end{subfigure} | |||
| \caption{Σύγκριση της μεθόδου για υψηλή πιθανότητα μετάλλαξης.} | |||
| \label{fig:constV_high_mut} | |||
| \end{figure} | |||
| \section{Συμπεράσματα} | |||
| Συνοψίζοντας, η χρήση του \textbf{γενετικού αλγορίθμου} για τη βελτιστοποίηση του χρόνου διέλευσης ενός οδικού δικτύου επέδειξε την ικανότητα των εξελικτικών τεχνικών να διαχειρίζονται σύνθετα προβλήματα χωρίς να απαιτούνται παράγωγοι ή άλλες αναλυτικές μέθοδοι. | |||
| Από την ανάλυση των αποτελεσμάτων, παρατηρήσαμε πως η \textbf{πιθανότητα μετάλλαξης} και το \textbf{μέγεθος του πληθυσμού} επηρεάζουν άμεσα τη σύγκλιση και την απόδοση του αλγορίθμου. | |||
| Μικρές πιθανότητες μετάλλαξης οδηγούν σε πιο αργή σύγκλιση, ενώ αυξημένος πληθυσμός παρέχει καλύτερη εξερεύνηση του χώρου λύσεων αλλά με μεγαλύτερο υπολογιστικό κόστος. | |||
| Τα αποτελέσματα δείχνουν πως μια \textbf{ισορροπημένη επιλογή παραμέτρων} επιτρέπει τη βέλτιστη κατανομή της κυκλοφορίας, μειώνοντας σημαντικά τον συνολικό χρόνο διάσχισης. | |||
| Επομένως, οι γενετικοί αλγόριθμοι αποτελούν μια αποτελεσματική επιλογή για παρόμοια προβλήματα βελτιστοποίησης, ειδικά όταν η διατύπωση του προβλήματος δεν επιτρέπει κλασικές μαθηματικές μεθόδους. | |||
| \end{document} | |||
BIN
Project/report/report.pdf
Ver arquivo
+ 0
- 90
Project/report/report.tex
Ver arquivo
| @@ -1,90 +0,0 @@ | |||
| % !TEX TS-program = xelatex | |||
| % !TEX encoding = UTF-8 Unicode | |||
| % !TEX spellcheck = el-GR | |||
| % | |||
| % Optimization techniques project report | |||
| % | |||
| % Requires compilation with pdfLaTeX or XeLaTeX | |||
| % | |||
| % authors: | |||
| % Χρήστος Χουτουρίδης ΑΕΜ 8997 | |||
| % cchoutou@ece.auth.gr | |||
| % | |||
| % Options: | |||
| % | |||
| % 1) mainlang=<language> | |||
| % Default: english | |||
| % Set the default language of the document which affects hyphenations, | |||
| % localization (section, dates, etc...) | |||
| % | |||
| % example: \documentclass[mainlang=greek]{AUThReport} | |||
| % | |||
| % 2) <language> | |||
| % Add hyphenation and typesetting support for other languages | |||
| % Currently supports: english, greek, german, frenc | |||
| % | |||
| % example: \documentclass[english, greek]{AUThReport} | |||
| % | |||
| % 3) short: Requests a shorter title for the document | |||
| % Default: no short | |||
| % | |||
| % example: \documentclass[short]{AUThReport} | |||
| % | |||
| \documentclass[a4paper, 11pt, mainlang=greek, english]{AUThReport} | |||
| \CurrentDate{\today} | |||
| % Document setup | |||
| %--------------------------------- | |||
| % \WorkGroup{Ομάδα Χ} | |||
| \AuthorName{Χρήστος Χουτουρίδης} | |||
| \AuthorMail{cchoutou@ece.auth.gr} | |||
| \AuthorAEM{8997} | |||
| %\CoAuthorName{Όνομα Επίθετο} | |||
| %\CoAuthorAEM{AEM} | |||
| %\CoAuthorMail{xxx@ece.auth.gr} | |||
| \DocTitle{Project: Γενετικοί αλγόριθμοι} | |||
| \DocSubTitle{Ελαχιστοποίηση συνάρτησης πολλών μεταβλητών} | |||
| \Department{Τμήμα ΗΜΜΥ. Τομέας Ηλεκτρονικής} | |||
| \ClassName{Τεχνικές Βελτιστοποίησης} | |||
| % | |||
| \InstructorName{Γ. Ροβιθάκης} | |||
| \InstructorMail{rovithak@auth.gr} | |||
| \CoInstructorName{Θ. Αφορόζη} | |||
| \CoInstructorMail{taforozi@ece.auth.gr} | |||
| % Local package requirements | |||
| %--------------------------------- | |||
| \usepackage{enumitem} | |||
| \usepackage{tabularx} | |||
| \usepackage{array} | |||
| \usepackage{multirow} | |||
| \usepackage{float} | |||
| \usepackage{xcolor} | |||
| \usepackage{soul} | |||
| \usepackage{amsmath} | |||
| \usepackage{footnote} | |||
| \usepackage{footmisc} | |||
| \begin{document} | |||
| \InsertTitle | |||
| %\tableofcontents | |||
| \section{Εισαγωγή} | |||
| Η παρούσα εργασία αφορά ... | |||
| \end{document} | |||
BIN
Project/scripts/figures/constV_pop_100mut_0.005.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_100mut_0.01.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_26mut_0.005.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_26mut_0.01.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_36mut_0.1.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_50mut_0.002.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_50mut_0.005.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_50mut_0.01.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_50mut_0.02.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_50mut_0.05.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_76mut_0.005.png
Ver arquivo
BIN
Project/scripts/figures/constV_pop_76mut_0.01.png
Ver arquivo
Project/scripts/main.m → Project/scripts/minimizeConstV.m
Ver arquivo
| @@ -20,25 +20,29 @@ normalizeSum = @(x, S) (x ./ sum(x)) * S; % Ensure sum of single row x equa | |||
| normalizeSum2 = @(x, S) (x ./ sum(x, 2)) * S; % Ensure sum of each row of 2D matrix x equals S | |||
| % Genetic Algorithm Parameters | |||
| popSize = 100; % Population size | |||
| popSize = 36; % Population size | |||
| maxGen = 2000; % Maximum number of generations | |||
| mutationRate = 0.05; % Mutation probability | |||
| mutationRate = 0.1; % Mutation probability | |||
| % Initialize Population | |||
| pop = rand(popSize, N) .* c; % Random initial solutions (0 <= x <= c) | |||
| pop = normalizeSum2(pop, V); % Ensure sum of each solution equals V | |||
| newPop = zeros(popSize, N); % Pre-allocate new population buffer | |||
| bestFitness = zeros(maxGen, 1); % Result array | |||
| % Genetic Algorithm Execution | |||
| for gen = 1:maxGen | |||
| % Fitness Calculation | |||
| fitness = arrayfun(@(i) fitnessFunction(pop(i, :), t, a, c, V, travelTime), 1:popSize); | |||
| % Selection | |||
| [~, idx] = sort(fitness); % Sort based on fitness (ascending order) | |||
| pop = pop(idx, :); % Retain the best solutions | |||
| % Keep the best chromosome | |||
| bestFitness(gen) = fitnessFunction(pop(1, :), t, a, c, V, travelTime); | |||
| % Crossover | |||
| newPop(1:popSize/2, :) = pop(1:popSize/2, :); % Retain top half | |||
| for i = 1:popSize/2 | |||
| @@ -63,14 +67,24 @@ for gen = 1:maxGen | |||
| pop = newPop; | |||
| end | |||
| % Final Solution | |||
| bestSolution = pop(1, :); | |||
| bestFitness = fitnessFunction(bestSolution, t, a, c, V, travelTime); | |||
| % Results | |||
| bestSolution = pop(1, :); | |||
| disp('Best Solution [veh/min]:'); | |||
| disp(bestSolution); | |||
| disp(['Best Objective Value: ', num2str(bestFitness), ' [min]']); | |||
| disp(['Best Objective Value: ', num2str(bestFitness(end)), ' [min]']); | |||
| figure('Name', 'Time over generations', 'NumberTitle', 'off'); | |||
| set(gcf, 'Position', [100, 100, 960, 640]); % Set the figure size | |||
| plot(1:maxGen, bestFitness, '-b', 'LineWidth', 1); | |||
| % Customize the plot | |||
| title(['Population = ', num2str(popSize), ' - Mutation = ', num2str(mutationRate)], 'Interpreter', 'latex', 'FontSize', 16); % Title of the plot | |||
| xlabel('Generations') ; | |||
| ylabel('T_{total}'); | |||
| % save the figure | |||
| print(gcf, ['figures/constV_pop_', num2str(popSize), 'mut_', num2str(mutationRate), '.png'], '-dpng', '-r300'); | |||
| % Fitness Function | |||
| function T_total = fitnessFunction(x, t, a, c, V, travelTime) | |||